Введение в цифровую графику
Усреднение в пределах интервала дискретизации
Ответ на заданный
выше вопрос можно сформулировать таким образом: непрерывный поток информации,
или непрерывный сигнал, подвергается разбиению на небольшие дискретные участки
с совершенно определенной целью — получить на этих участках один-единственный
отсчет (дискретный элемент). Сама по себе эта процедура, конечно, ничего не
решает, но создает предпосылку для последующих шагов.
В качестве следующего
шага необходимо выяснить, как в пределах интервала получить одно значение, один
дискретный элемент?
Для того чтобы
получить единственное значение в пределах этого "дискретного интервала",
необходимо просто-напросто усреднить сигнал между границами этих "дискретов"
(рис. 6.4).
Таким образом,
следущий шаг этапа дискретизации — это усреднение, или интегрирование, непрерывно
изменяющегося сигнала в пределах каждого отсчета.

Рис.
6.4. Усреднение сигналов в пределах "дискретов"
Замечание
В содержательном смысле превращение фрагмента непрерывного сигнала в одно-единственное значение является нетривиальной процедурой. Действительно, как выбрать наиболее характерное значение? Если бы анализом и отбором занимались люди, например музыканты, то понятно, что при очень небольшой производительности качество приближалось бы к оптимально художественному. На самом деле, для технической реализации необходимо применить стандартизированный прием, например использовать текущее значение в момент "биения" метронома. Этот нюанс уже зависит от конкретного технического решения.
Но поскольку за
эту интеграцию "отвечает" вычислительная техника, необходимо принять
максимально простой алгоритм. А самой простой процедурой в этой ситуации является
усреднение (хотя возможен выбор минимального или максимального значения в интервале).
Пример-метафора
Предположим, что
в учебной канцелярии возникла необходимость сравнить успеваемость двух групп.
Как это сделать? Понятно, что в обеих группах есть "отличники" и "двоечники",
т. е. существует определенный разброс оценок по разным дисциплинам. Если же
будут выбраны усредненные значения, не учитывающие разброса, то в общем (с неизбежными
погрешностями) мы получим основания для того, чтобы сравнивать, т. к. располагаем
дискретными значениями. Скажем, в одной группе средний балл получился равным
4,9, а в другой — 3,1. Понятно, что первая группа по успеваемости значительно
превосходит вторую, хотя для двух конкретных студентов из этих групп это соотношение
может быть несправедливым.
Конечно, в этом
алгоритме есть недостатки, которые являются неизбежной платой за возможность
сравнения. В той группе, где средний балл оказался равным 3,1, отдельный студент
может иметь пятерки по всем предметам. Невзирая на это, вся группа числится
в отстающих. Кого-то это может не устраивать, но такова объективная реальность,
таков механизм, таков алгоритм.
Замечание
Этот алгоритм не носит, впрочем, всеобщего характера. Возможны и анекдотические случаи: скажем, средняя температура по больнице.
В результате усреднения
(интеграции) сигнала в пределах диапазона дискретизации на графике появится
множество средних значений. На каждом дискретном участке они отображаются линиями,
параллельными горизонтальной оси.
Пример-метафора
Представьте себе
график прибылей какого-либо предприятия. Этот график отображает информацию о
каждом рабочем дне. Для прогнозирования необходима обобщенная информация, например
помесячно.
Но с помощью такого
ежедневного графика невозможно сравнивать помесячные доходы друг с другом (вспомните
успеваемость группы по отдельным учащимся и по отдельным предметам), значения
по дням имеют очень значительный разброс. Поэтому необходимо определить усредненные
значения прибыли за каждый месяц. В результате вместо ежедневного графика получается
график помесячный, который наглядно отображает уровни прибылей.
Стоит обратить
внимание, что после процедуры усреднения аналоговый сигнал преобразуется в ступенчатую
линию, которая, в общем, конечно, имитирует исходную кривую (рис. 6.5).
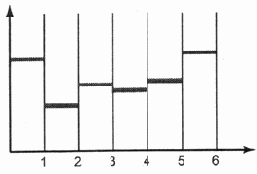
Рис.
6.5. Вид ступенчатой линии сигнала после усреднения
На данном этапе
можно уточнить определение дискретизации.
Определение
Дискретизация — это разделение на участки, в которых сигнал усредняется, В этом случае определяются отдельные, независимые друг от друга отсчеты, которые можно сравнивать между собой.
Усредненные значения — необходимый этап конвертирования аналогового сигнала в цифровой, но не конечный, а промежуточный. Следующим этапом является сравнение полученных значений по специальной шкале, т. е. квантование.