Введение в цифровую графику
Расчет количества кодов
"Ой, теперь
он и тебя сосчитал!" — заскулил Теленок.
Альф Прейсен
Эту задачу по
расчету количества кодов стоит обсудить подробнее, поэтому с целью упрощения
моделируем ситуацию кодирования чисел с помощью электрических лампочек. Каждая
лампочка представляет собой разряд двоичного числа.
Замечание
С той же целью упрощения мы исключаем временной параметр, т. е. лампочки с течением времени не изменяют своего состояния.
Сначала представьте
себе, что в нашем распоряжении имеется одна-единственная электрическая лампочка,
с помощью которой необходимо обозначить какую-либо информацию.
Сколько отдельных
кодов можно смоделировать с помощью одной лампочки? Совершенно очевидно, что
она может иметь только два состояния: "горит" или "не горит".
И других состояний быть не может (мы, разумеется, не учитываем ситуацию, когда
лампочка неисправна или в цепи нет тока).
Пример-метафора
Разрыв тока в
цепи используется для сигнализации в мелких торговых предприятиях или офисах.
Если сигнальная лампочка горит, это свидетельствует о том, что объект в сохранности...
Говоря математически,
отвлекаясь от качественного содержания (магазинов, грабителей и пр.), можно
сказать, что с помощью одной лампочки (одного разряда или одного бита) удается
кодировать два значения, например "ноль" или "единицу" (рис.
5.1).
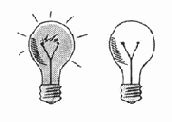
Рис.
5.1. Коды, создаваемые с помощью одной лампочки
Теперь усложняем
задачу: используем два разряда, или, в нашей "научной" терминологии
— две лампочки. Сколько сигналов, или кодов, мы можем с их помощью обеспечить?
Это зависит от
того, сколько комбинаций (битовых "слов") мы можем составить.
Замечание
В обычных словах играет роль последовательность элементов-букв. Когда мы говорим слово "да", мы используем две буквы — но сигнал-то один, т. к. обозначается одно конкретное слово. Эти две буквы сами по себе ничего не значат, кроме звуков. Только их сочетание имеет значение, дает тот самый код, который имеет соответствующий смысл. Если мы переставим элементы, то получим совсем другое слово — "ад", что характерно, не имеющее никакой связи с первым. Когда мы говорим "нет", мы используем три буквы, которые также сами по себе ничего не значат. Поэтому мы должны считать не буквы, а сочетания. Это напоминает позиционный принцип: если мы ставим один и тот же элемент (одну и ту же букву, цифру или, как в данном случае, одну и ту же лампочку) в разные позиции или их разные сочетания — мы получаем разные значения кодов.
Итак, рассмотрим
все возможные комбинации.
- Первый сигнал:
обе лампочки выключены.
- Второй сигнал:
включена только одна лампочка слева.
-
Третий сигнал: включена только одна лампочка справа.
- Четвертый
сигнал: обе лампочки включены.
Желающие могут
проверить: других вариантов не получится (рис. 5.2)! Следовательно, когда приходится
использовать две лампочки (или два двоичных разряда), всегда получаются четыре
кода.
До сих пор все
кажется достаточно очевидным, но следующий шаг ("рассмотрим более сложный
вариант из трех лампочек, или трех разрядов") всегда вызывает в аудиториях,
далеких от математики, ошибочные мнения. Обычно чаще всего называют числа "6"
или "9" (видимо, по аналогии: "три плюс три" или "три
в квадрате"). И то и другое — ошибка.
Для преодоления
ошибки составим таблицу, представив горящую лампочку "единицей", а
негорящую — "нулем" (табл. 5.1).
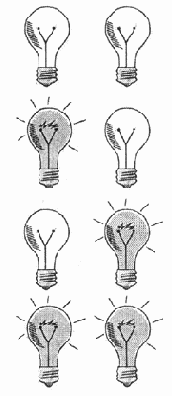
Рис. 5.2. Коды, создаваемые с помощью двух лампочек
Таблица
5.1. Количество кодов, создаваемых тремя двоичными разрядами
|
Номер
по порядку |
Двоичный
код |
Номер
по порядку |
Двоичный
код |
||
|
1 |
000 |
5 |
100 |
||
|
2 |
001 |
6 |
101 |
||
|
3 |
010 |
7 |
110 |
||
|
4 |
011 |
8 |
111 |
||
В результате получилось
восемь кодов, которые представляют диапазон от "все лампочки потушены"
до "все лампочки горят".
Мы не зря использовали
условные обозначения для лампочек ("ноль" и "единицу"),
ведь по сути дела нам требовалось написать двоичные числа, которые являются
кодами десятичных чисел от "О" до "7". Для этого требуется
два двоичных разряда.
Можно продолжить
наращивание количества разрядов и составить таблицу кодов для четырех двоичных
разрядов (табл. 5.2).
Таблица
5.2. Количество кодов, создаваемых четырьмя двоичными разрядами
|
Номер
по порядку |
Двоичный
код |
Номер
по порядку |
Двоичный
код |
||
|
1 |
0000 |
9 |
1000 |
||
|
2 |
0001 |
10 |
1001 |
||
|
3 |
0010 |
11 |
1010 |
||
|
4 |
0011 |
12 |
1011 |
||
|
5 |
0100 |
13 |
1100 |
||
|
6 |
0101 |
14 |
1101 |
||
|
7 |
0110 |
15 |
1110 |
||
|
8 |
0111 |
16 |
1111 |
||
В результате получилось
шестнадцать кодов, которые также представляют диапазон от "все лампочки
потушены" до "все лампочки горят", т. е. десятичные числа от
"О" до "15".
Полагаем, что
дальше продолжать нет необходимости: принцип получения кодов, кажется, ясен,
и теперь можно составить таблицу (табл. 5.3) зависимости между количеством двоичных
разрядов (битов) и количеством кодов, которые можно получить с их помощью.
Таблица
5.3. Количество разрядов и количество кодов
|
Количество
разрядов двоичного числа |
Количество
кодов |
Количество
разрядов двоичного числа |
Количество
кодов |
||
|
1 |
2 |
6 |
64 |
||
|
2 |
4 |
7 |
128 |
||
|
3 |
8 |
8 |
256 |
||
|
4 |
16 |
9 |
512 |
||
|
5 |
32 |
10 |
1024 |
||
Обратите внимание
на то, что каждое последующее количество кодов больше предыдущего в два раза.
Это означает, что количество разрядов является степенью при основании "двойки".
Если значение степени равняется количеству
разрядов, то общее количество кодов можно вычислить по чрезвычайно простой формуле:
N=2n, где
N — это количество кодов, а n — количество двоичных разрядов.
С помощью приведенной
формулы всегда можно определить, сколько потенциальных кодов получается в случае
использования определенного количества разрядов.
Не стоит забывать,
что эти рассуждения интересуют нас исключительно в связи с компьютерными технологиями,
т. к. каждый разряд требует аппаратного размещения. Отсюда можно поставить обратную
задачу: как рассчитать количество разрядов, если известно количество кодов,
которое необходимо обеспечить для кодирования известной совокупности данных.