Системы координат

Все программы ЗD-графики, прежде всего, позволяют использовать декартову (картезианскую) систему координат (Cartesian coordinate system) (рис. 13.1), которую мы уже упоминали выше.

Более подробно о декартовой системе координат см. в части III.

В этой системе координат положение произвольной точки Р в пространстве задается тремя

вещественными числами (координатами), обозначающими перпендикулярные проекции этой точки на три фиксированные, взаимоперпендикулярные, градуированные линии, называемые осями координат.

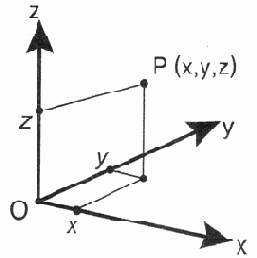
Рис. 13.1. Картезианская система координат

Обычно эти три оси координат (coordinate axis) обозначаются как ось х (абсцисса), ось у (ордината) и ось z (аппликата), а отложенные на них координаты точки записываются как (х, у, z).

Точка с координатами (0, 0, 0) называется началом системы координат (origin).

Также надо заметить, что существует два варианта таких прямоугольных систем координат: правосторонняя и левосторонняя. Чтобы разобраться в них, достаточно нарисовать на листе бумаги ось х горизонтально (положительные значения отложены справа от начала координат), а ось у вертикально (положительные значения сверху от начала координат). Теперь, если на оси z, проведенной перпендикулярно плоскости листа, положительные значения идут от листа к зрителю, то это правосторонняя система координат. В противном случае система координат — левосторонняя.

Реже, но все же достаточно часто, используются две другие системы координат: полярная цилиндрическая система координат (polar cylindrical coordinate system) и полярная сферическая система координат (polar spherical coordinate system).

В цилиндрической системе координат (рис. 13.2) положение точки в пространстве также описывается тремя координатами (r, 0, z):

r— это расстояние от начала координат (точки 0) до проекции точки Р на плоскость ху;
0 — это угол между фиксированной плоскостью xz и полуплоскостью, проходящей через точку Р и ось z,
z — расстояние от точки Р до плоскости ху.

В сферической системе координат (рис. 13.3) положение точки в пространстве задается тремя координатами (r, 0, р):

r — расстояние от начала координат;
углом 0 (азимут) между фиксированной плоскостью xz и полуплоскостью, проходящей через точку Р и ось z,
углом р (зенит) между фиксированной полярной полуосью Oz и лучом, проведенным через начало координат (точку 0) и точку Р.

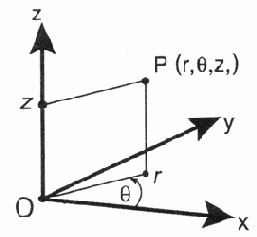
Рис. 13.2. Цилиндрическая система координат

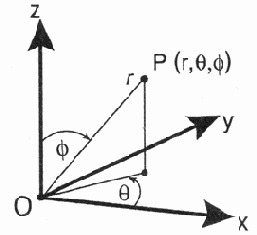
Рис. 13.3. Сферическая система координат

Отметим, что координаты точки могут быть взаимнооднозначно пересчитаны из одной системы координат в другую.

Пример

Например, пересчет из полярной сферической системы координат в картезианскую будет выглядеть так:

х = rsin0-cos p;

у = r-sin0-sir p; z = r-cos0.

Содержание раздела