Введение в цифровую графику
Параметрические уравнения
Как уже было сказано
выше, кривые можно представлять аналитически и графически, т. е. как график
функции. Математики записывают это следующим образом:
что означает "значение
у — это функция, т. е. зависимость, от значения х", например
простейшая функция у = 2х означает простейшую зависимость: каждое значение
у в два раза больше любого значения х. График этой функции представляет
собой прямую линию, проходящую через начало координат (рис. 12.2).
Более интересный
вид представляют собой тригонометрические функции, например синусоида:
у
= sin х. График такой кривой известен каждому (рис. 12.3).
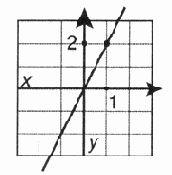
Рис.
12.2. График функции у = 2х
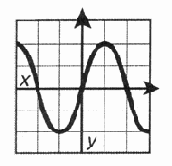
Рис.
12.3. График функции у = sinx
Такой способ представления
формулы и ее графика называется явным. Он позволяет относительно легко строить
график. Однако у этого способа с точки зрения графического представления имеются
весьма существенные недостатки.
- Каждому
значению х соответствует только одно значение у. Это не дает
возможности начинать новый фрагмент кривой в произвольном месте.
- Кривая не
может быть замкнутой.
В результате явный
способ представления не может применяться там, где требуется описание произвольных
кривых, размещаемых в произвольных местах на плоскости.
Альтернативным
способом является определение кривой как параметрической функции.
В первую очередь
очень важно отметить следующую особенность: у такого способа обе координаты
(х и у) являются равноправными, т. е. вычисляются как функции
некоего вспомогательного параметра, обозначаемого, как правило, символом t.
В общем случае такая зависимость получает вид:
q(t) =
{x(t), y(t)},
где х(t) и y(f)
— функции параметра t.
Задавая одинаковые
значения t, функция x(f) вычисляет значения координаты х, а функция
y(t) — значения координаты у.
Пример-метафора
Можно легко представить,
что значения параметра t— это отсчеты времени, в течение которого происходит
перемещение определенной частицы вдоль произвольной кривой, например окружности.
Параметрическая функция q(t) позволит
получать пары координат {х, у}, по которым перемещается частица в различные
моменты (значения) времени f. Хотя, в общем случае, не обязательно параметр
t связывать со временем.
Вторым важным
качеством параметрических кривых является то, что они имеют более разнообразные
формы, чем это позволяют явные уравнения.
Пример
Графики синусоиды и косинусоиды в явном виде не позволяют замкнуть линию, а две параметрические функции
x(f) = cost;
y(t) = sinf
создают окружность, если t "пробегает" значения между 0 и 360 градусов.
Справка
Параметрическое представление функции — это выражение функциональной зависимости между несколькими переменными введением вспомогательных переменных, которые принято называть "параметрами". Если мы располагаем двумя переменными, например по оси х и по оси у, то зависимость между ними можно рассматривать как уравнение плоской кривой. Например, координаты х и у точек этой кривой определяются каким-то параметром, скажем, величиной t, которую определяют как некоторый диапазон. Особенно важно такое представление для пространственных кривых, поскольку обеспечивает более легкий способ построения графиков.
Применение параметрических
функций позволяет применять более сложные функции, а не только линейную аппроксимацию,
поскольку одним из основных недостатков аппроксимации прямыми является, как
уже указывалось, наличие угловых изгибов, которые даже при относительно невысоком
увеличении не создают впечатления гладкости. Поэтому неизбежной заменой прямолинейным
сегментам могут быть только кривые, которые способны обеспечить требуемую гладкость
(забегая вперед, можно указать, что речь идет о кривых Безье и NURBS-кривых).
Но сначала необходимо более точно определить понятие гладкости.
