Введение в цифровую графику
Канонический вид кривой Безье
Рассмотрим канонический
вид кривой Безье и попытаемся понять, как из одной-единственной кривой получается
бесконечно большое многообразие форм, которые используются в векторной компьютерной
графике.
Общий вид кривой
Безье имеет вот такую конструкцию (рис. 12.25).
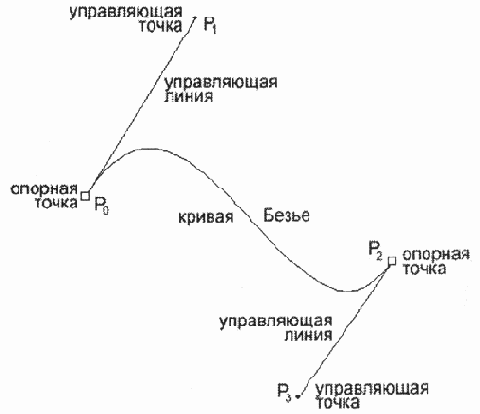
Рис.
12.25. Канонический вид кривой Безье
Причем, это уже
не математическое описание, а сугубо прикладное отображение, именно то, которое
знакомо всем пользователям векторных программ.
Замечание
Такое отображение все чаще используется и в программах пиксельной графики, а также в программах верстки.
Для построения
этой кривой требуются четыре контрольные точки. Но кривая физически проходит
только через две из них, они получили название опорных. Одна из точек
называется начальной (start point), а другая — конечной (end point).
Две точки остаются в стороне, они получили название управляющих (control
point).
И для того чтобы
их не "потерять" (особенно когда в документе кривых насчитываются
многие десятки и сотни), в программах векторной графики, да и в любых других
программах, управляющие точки соединяются с опорными точками какой-нибудь линией.
Иногда пунктирной, иногда тонкой сплошной.
Почему кривая
располагает начальной и конечной точками? Потому что, вообще говоря, кривая
Безье — это, прежде всего, вектор.
Справка
Слово "вектор" латинского происхождения: "vector" переводится как "несущий", в математике используется для обозначения отрезка определенной длины и направления. Два вектора считаются равными лишь в том случае, если у них не только одинаковы длины, но и совпадают направления (то есть они параллельны и одинаково ориентированы). При изменении направления меняется знак вектора. В естественных науках векторы изображают величины, которые имеют направление, например сила, скорость, ускорение и т. д.
Направление кривой,
может быть, не всегда очевидно для пользователей векторной программы, но для
самой программы оно всегда существенно. Направление контуров находит свою реализацию
в так называемых составных контурах (compound paths). Если два векторных объекта,
например образующих букву "о" и расположенных друг на друге, направлены
в противоположные стороны (рис. 12.26), то изображение получится верное ("с
дыркой посередине").
Если те же векторные
контуры направлены в одну сторону, то в этом случае один контур просто перекрывает
другой, не образуя прозрачной области (рис. 12.27).
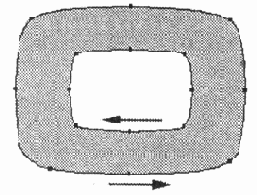
Рис.
12.26. Составной контур с разнонаправленными векторами
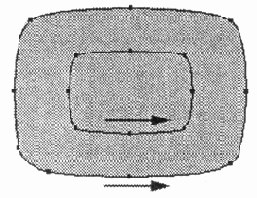
Рис. 12.27. Составной контур с однонаправленными векторами