Введение в цифровую графику
Свойства кривых Безье
Кривые Безье любой
степени обладают следующими важными свойствами. П Начальная и конечная
контрольные точки лежат на кривой.
- Кривая на
всем протяжении непрерывна, у нее отсутствуют разрывы. Это важнейшее свойство,
без которого кривая Безье вообще бы не рассматривалась.
- Касательные
к кривой в начальной и конечной контрольных точках являются отрезками, соединяющими
их с другими двумя соседними контрольными точками, через которые в общем случае
кривая не проходит.
- Точки на краях
касательных будут располагаться на кривой только в том случае, если последняя
представляет собой прямую линию.
- Поскольку
кривая Безье представляет собой взвешенное усреднение всех ее контрольных
точек с положительными весами, а сумма их равна единице, кривая всегда располагается
внутри выпуклого многоугольника из ее контрольных точек (рис. 12.20), как
и рассмотренная выше NURBS-кривая.
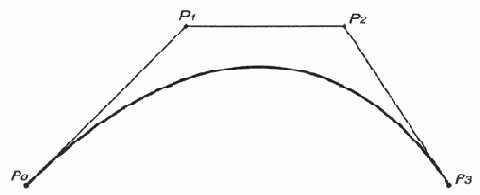
Рис.
12.20. Кривая в выпуклом многоугольнике
- Кривую Безье
можно рассматривать как пошаговое уточнение формы многоугольника, получаемого
последовательным соединением ее контрольных точек (рис. 12.21—12.24). При
этом кривая Безье начинается и заканчивается в конечных точках данного многоугольника,
а форма определяется относительным расположением оставшихся точек, через которые
в общем случае она не проходит.
Исходя из этого
можно представить канонический вид кривой Безье, который обычно используется
в графических редакторах плоской графики.
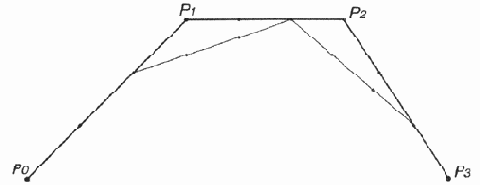
Рис.
12.21. Первый этап аппроксимации кривой
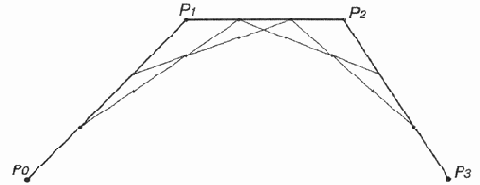
Рис.
12.22. Второй этап аппроксимации кривой
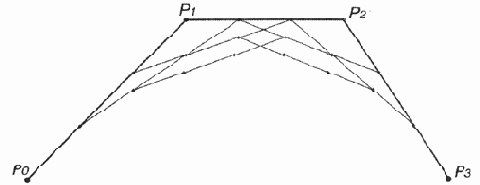
Рис.
12.23. Третий этап аппроксимации кривой
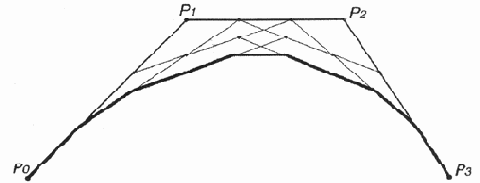
Рис. 12.24. Итоговая ломаная кривая