Введение в цифровую графику
Кривая Безье (формулы и принципы построения)
В общем случае
кривая Безье — это частный случай В-СПЛЗЙНОВ (NURBS-кривых), которые можно определить
как взвешенная сумма п+ 1 контрольных точек, где весовыми коэффициентами
являются полиномы Бернштейна. Рассмотрим определения первых трех степеней кривой
Безье.
Линейная кривая,
кривая первой степени (прямая), определяется следующей параметрической формулой:
P(t) =
(1 - t)P0+tP1
Это выражение
представляет собой линейную интерполяцию между двумя точками (рис. 12.17).
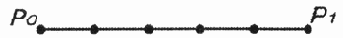
Рис.
12.17. Кривая первой степени (прямая)
Квадратичная кривая,
кривая второй степени, определяется формулой:
= (1 - t)2P0
+ 2(1 - t)tP1 + t2P2.
Это выражение
представляет собой линейную интерполяцию между линейными интерполяциями между
точками (рис. 12.18):
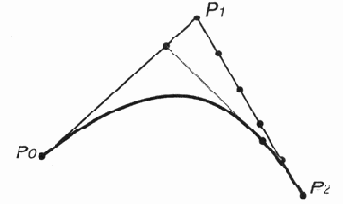
Рис.
12.18. Кривая второй степени (квадратическая кривая)
Кубическая кривая,
кривая третьей степени, определяется формулой: P(t) = (1 - t)3Р0
+ 3(1 - t)2tP1 + 3(1 - t)t2P2
+ t3Р3.
Это выражение
представляет собой линейную интерполяцию между линейными интерполяциями между
линейными интерполяциями между точками (рис. 12.19).
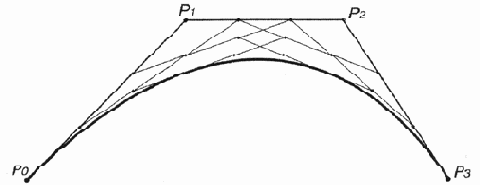
Рис. 12.19. Кривая третьей степени (кубическая кривая)