Алгоритмическому

Эвристические решения, методы основываются на связанных с задачей специальных знаниях, простейших правилах, интуитивных критериях, базирующих на предыдущем опыте и на других ненадежных методах вплоть до угадывания. Эвристические методы не всегда приводят к цели, даже когда решение существует, или они могут привести к неверному решению.

Когда используются эвристические методы?

·        Неизвестен алгоритм.

·        Доказано отсутствие алгоритмического решения.

·        Существуют ограничения, налагаемые вычислительной техникой.

На основе эвристических решений, во многих случаях, потихоньку изобретаются алгоритмы. Эвристические программы в своей реализации базируются на алгоритмах.

Формулировка игровых задач в терминах И/ИЛИ-графов

Такие игры, как шахматы или шашки, естественно рассматривать как задачи, представленные И/ИЛИ-графами. Игры такого рода называются играми двух лиц с полной информацией. Будем считать, что существует только два возможных исхода игры: ВЫИГРЫШ и ПРОИГРЫШ. (Об играх с тремя возможными исходами - ВЫИГРЫШ, ПРОИГРЫШ и НИЧЬЯ, можно также говорить, что они имеют только два исхода: ВЫИГРЫШ и НЕВЫИГРЫШ). Так как участники игры ходят по очереди, мы имеем два вида позиций, в зависимости от того, чей ход. Давайте условимся называть участников игры "игрок" и "противник", тогда мы будем иметь следующие два вида позиций: позиция с ходом игрока ("позиция игрока") и позиция с ходом противника ("позиция противника"). Допустим также, что начальная позиция P - это позиция игрока. Каждый вариант хода игрока в этой позиции приводит к одной из позиций противника Q1, Q2, Q3, … (рис. 2.10).

Рис. 2.10. Формулировка игровой задачи для игры двух лиц

 в форме И/ИЛИ-дерева; участники игры: "игрок" и "противник"

Далее, каждый вариант хода противника в позиции Q1 приводит к одной из позиций игрока R11,  R12, … . В И/ИЛИ-дереве, показанном на       рис. 2.10, вершины соответствуют позициям, а дуги - возможным ходам. Уровни позиций игрока чередуются в дереве с уровнями позиций противника. Для того чтобы выиграть в позиции P, нужно найти ход, переводящий позицию P в выигранную позицию Qi (при некотором i). Таким образом, игрок выигрывает в позиции P, если он выигрывает в  Q1 или Q2, или Q3, или … . Следовательно,  P - это ИЛИ-вершина. Для любого i, позиция Qi - это позиция противника, поэтому если в этой позиции выигрывает игрок, то он выигрывает и после каждого варианта хода противника. Другими словами, игрок выигрывает в Qi, если он выигрывает во всех позициях Ri1 и Ri2 и … . Таким образом, все позиции противника - это И-вершины. Целевые вершины - это терминальные (окончательные) позиции, выигранные согласно правилам игры, например, позиции, в которых король противника получает мат.
Позициям проигранным соответствуют задачи, не имеющие решения. Для того чтобы решить игровую задачу, мы должны построить решающее дерево, гарантирующее победу игрока независимо от ответов противника. Такое дерево задает полную стратегию достижения выигрыша: для каждого возможного продолжения, выбранного противником, в дереве стратегии есть ответный ход, приводящий к победе.

Ниже приводится простая программа, которая определяет, является ли некоторая позиция игрока выигранной.

'выигранная'(P):-

         'терм_выигранная'(P). % терминальная выигранная позиция

'выигранная'(P):-

         not 'терм_проигранная'(P), % не терминальная проигранная

                                                       % позиция

         'ход'(P,P1),          % разрешенный ход из позиции P в позицию P1

         % ни один из ходов противника не ведет к не-выигрышу

         not('ход'(P1,P2),

               not 'выигранная'(P2)).

Здесь правила игры встроены в предикат 'ход'(P,P1), который порождает все разрешенные ходы, а также в предикаты 'терм_выигранная'(P)  и 'терм_проигранная'(P), которые распознают терминальные позиции, являющиеся, согласно правилам игры, выигранными или проигранными. В последнем из правил программы, содержащем двойное отрицание, говорится: не существует хода противника, ведущего к не выигранной позиции. Другими словами, все ходы противника приводят к позициям, выигранным с точки зрения игрока.

Программа, которую мы составили, демонстрирует основные принципы программирования игр. Но практически приемлемая реализация таких сложных игр, как шахматы или го, потребовала бы привлечения значительно более мощных методов. Огромная комбинаторная сложность этих игр делает наш наивный переборный алгоритм, просматривающий дерево вплоть до терминальных игровых позиций, абсолютно непригодным. Для шахмат, например, пространство поиска имеет астрономические размеры - около 10120 позиций.

Фреймы

Этот термин введен М. Минским для обозначения минимальной структуры, описывающей некоторое понятие или объект. Фрейм имеет имя (название) и состоит из частей, обычно называемых слотами; изображается фрейм в виде цепочки:

Фрейм = <слот 1><слот 2>…<слот N>.

Слот представляет собой пару атрибут (имя слота) — значение. В качестве значения могут выступать константные факты, выражения, содержащие переменные, ссылки на другие слоты, ссылки на фреймы и т. п.

Поэтому фрейм является рекурсивной структурой.

Рассмотрим в качестве примера фрейм "Битва". Цепочка этого фрейма выглядит так:

Битва = <кто?><с кем?><когда?><где?><результат>.

Представленный фрейм называется фреймом-прототипом. Во фреймах такого вида слоты имеют переменные значения. Например:

Битва = <Герой><Антигерой><утром><в чистом поле><победил>.

В этом случае, по крайней мере, слоты Герой и Антигерой - переменные, их значения могут уточняться. В результате такого уточнения получается фрейм-экземпляр:

Битва = <Царевич><Кощей Бессмертный><утром><в чистом поле><победил>.

Исключение из фрейма любого слота делает его принципиально неполным, иногда бессмысленным и не соответствующим названию фрейма.

Для автоматизированной обработки фреймов создан ряд языков, таких, например, как KPL, FPL. Близкое к понятию фрейма понятие объекта реализовано в объектно-ориентированном программировании.

Частным случаем фреймов являются скрипты, представляющие собой описание стереотипного сценария действия с участием определенных объектов. Скрипты связаны с текущей культурой и необходимым знанием для понимания таких предложений "Я вошел в ресторан, официантка принесла мне меню". Они могут вызывать другие скрипты и обладают большими, чем фреймы, возможностями для описания динамических аспектов знания.

Функции и структура экспертной системы

Экспертная система - это программа, которая ведет себя подобно эксперту в некоторой, обычно узкой, прикладной областью. Типичные применения экспертных систем включают в себя такие задачи, как медицинская диагностика, локализация неисправностей в оборудовании и интерпретация результатов измерений. Экспертные системы должны решать задачи, требующие для своего решения экспертных знаний в некоторой конкретной области. В той или иной форме экспертные системы должны обладать такими знаниями. Поэтому их также называют системами, основанными на знаниях. Однако не всякую систему, основанную на знаниях, можно рассматривать как экспертную. Экспертная система должна также уметь каким-то образом объяснять свое поведение и свои решения пользователю, так же, как это делает эксперт-человек. Это особенно необходимо в областях, для которых характерна неопределенность, неточность информации (например, в медицинской диагностике). В этих случаях способность к объяснению нужна для того, чтобы повысить степень доверия пользователя к советам системы, а также для того, чтобы дать возможность пользователю обнаружить возможный дефект в рассуждениях системы. В связи с этим в экспертных системах следует предусматривать дружественное взаимодействие с пользователем, которое делает для пользователя процесс рассуждения системы "прозрачным".

Часто к экспертным системам предъявляют дополнительное требование - способность иметь дело с неопределенностью и неполнотой. Информация о поставленной задаче может быть неполной или ненадежной; отношения между объектами предметной области могут быть приближенными. Например, может не быть полной уверенности в наличии у пациента некоторого симптома или в том, что данные, полученные при измерении, верны; лекарство может стать причиной осложнения, хотя обычно этого не происходит. Во всех этих случаях необходимы правдоподобные рассуждения.

Можно выделить два типа экспертных систем:

·        для специалистов невысокого профессионального уровня (экспертная система хранит знания, полученные от специалистов экстракласса);

·        для специалистов высокого класса - поиск и просмотр больших массивов информации и выполнение рутинных операций.

В самом общем случае для того, чтобы построить экспертную систему, мы должны разработать механизмы выполнения следующих функций системы:

·        решение задач с использованием знаний о конкретной предметной области - возможно, при этом возникнет необходимость иметь дело с неопределенностью;

·        взаимодействие с пользователем, включая объяснение намерений и решений системы во время и после окончания процесса решения задачи.

Каждая из этих функций может оказаться очень сложной и зависит от предметной области, а также о различных практических требований.

При разработке экспертной системы принято делить их на три модуля, как показано на рис. 3.1:

(1)  база знаний;

(2)  машина логического вывода;

(3)  интерфейс с пользователем.



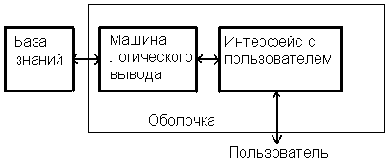Рис. 3.1. Структура экспертной системы

База знаний содержит знания, относящие к конкретной прикладной области, в том числе отдельные факты, правила, описывающие отношения или явления, а также возможно, методы, эвристики и различные идеи, относящиеся к решению задач в этой прикладной области. Машина логического вывода умеет активно использовать информацию, содержащую в базе знаний. Интерфейс с пользователем отвечает за бесперебойный обмен информацией между пользователем и системой; он также дает пользователю возможность наблюдать за процессом решения задач, протекающим в машине логического вывода. Принято рассматривать машину вывода и интерфейс как крупный единый модуль, обычно называемой оболочкой экспертной системы, или, для краткости, просто оболочкой.

В  описанной выше структуре собственно знания отделены от алгоритмов, использующих эти знания. Такое разделение удобно по следующим соображениям. База знаний, очевидно, зависит от конкретного приложения.С другой стороны, оболочка, по крайней мере, в принципе, независима от приложений. Таким образом, разумный способ разработки экспертной системы для нескольких приложений сводится к созданию универсальной оболочки, после чего для каждого приложения достаточно подключить к системе новую базу знаний. Разумеется, все эти базы знаний должны удовлетворять одному и тому же формализму, который оболочка "понимает". Практический опыт показывает, что для сложных экспертных систем наш сценарий с одной оболочкой и многими базами знаний работает не так гладко, как бы этого хотелось, за исключением тех случаев, когда прикладные области очень близки. Тем не менее, даже если переход от одной прикладной области к другой требует модификации оболочки, то, по крайней мере, основные принципы ее построения обычно удается сохранить.

Изменение представлений

Поиск хорошего представления знаний в ходе решения задачи является почти всегда необходимым этапом на пути к решению.

Задача о четырех шахматных конях

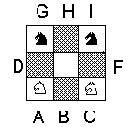Как за минимальное число ходов изменить на противоположное положение двух черных и двух белых коней? В задаче используется шахматная доска 3´3. Исходная позиция задачи о четырех конях представлена на        рис. 1.3. Кони ходят (перемещаются по доске) привычным образом. Центральная клетка имеет метку E.

  

Рис. 1.3. Исходная позиция в задаче о 4 конях

При знакомстве с задачей нашим первым побуждением является сделать несколько попыток по перемещению коней на настоящей шахматной доске, но интуитивно мы понимаем, что, что имеется слишком много вариантов получения конечной позиции, причем при таком подходе плохо используется симметрия, присущая этой задаче. Пытаясь промоделировать условия задачи на уровне какого-то более общего представления, первое, о чем мы вспоминаем, это декартова система координат. Однако такое представление имеет существенный недостаток, связанный с трудностью записи перемещения фигур "ходом коня". Однако такие перемещения очень важны в нашем случае и именно они-то и должны быть представлены в удобной форме. Сама по себе шахматная доска почти не играет в задаче существенной роли, и ее физическое представление является только внешней поддержкой решения задачи, так как на самом деле единственно существенным является учет связей между ходами, сделанными при переходе от позиции к позиции. Мы знаем, что черный конь может переместиться на поле A за один ход с поля H или поля F. В свою очередь на поле H конь сможет попасть либо с того же поля A, либо с поля C, на поле C - с поля D, на него - с поля I, на поле I - с поля B, на него - с поля G и, наконец, на G - с поля F, начиная с которого конь сможет вновь попасть на поле A. Этот маршрут в виде окружности, проходящей в указанном порядке через все позиции, изображен на рис. 1.4.

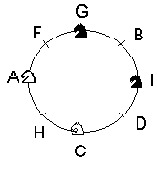Рис. 1.4.
Решение задачи о 4 конях

Представление, получаемое с помощью этой диаграммы, наглядно и удобно для использования. На рисунке не представлено поле E, но это соответствует реальной ситуации - ни при каком ходе коня ни в одной позиции оно недостижимо. Все другие ситуации отражены, и это позволяет использовать ту же кольцевую диаграмму и для других коней.

Новая формулировка задачи теперь состоит в том, что нужно так переместить по этой окружности черных коней на A и C, а белых коней на G и I, чтобы за один ход конь перемещался на одну позицию справа или слева по окружности. Решение задачи теперь практически очевидно: достаточно лишь повернуть на пол-оборота весь ансамбль фигур так, чтобы C попало на G, A - на I, G - на C и I - на A. Это вращение, которое соответствует четырем ходам каждого коня, или шестнадцати ходам всех фигур, дает решение задачи - минимальное число ходов для изменения исходной позиции на противоположную.

 

Изменения представления знаний во время решения задачи - основной путь ее решения.

В представлении знаний при решении математических задач существенным является то, о чем не говорится в учебниках по математике и на лекциях, а именно каким образом и как находят доказательство.

На самом деле способ действия математика включает три различные фазы:

1.     Понять теорему, заданную на формальном языке, т.е. перевести ее в некоторое внутреннее представление.

2.     Доказать теорему в этом внутреннем представлении, используя для этого все накопленные и адаптированные к этому внутреннему представлению знания.

3.     Перевести найденное еще не полное доказательство в строгое математическое доказательство, вновь введя символическую формализацию обычного математического языка.

Мы будем использовать логический подход в изучении ИИ, хотя он и имеет большие ограничения (см. раздел  1.4. Психологическая теория интеллекта). Представлять знания мы будем с помощью формул логики предикатов первого порядка, и использовать логический вывод.Конкретным инструментом для программирования будет язык SWI-prolog (см. курс лекций по логическому программированию). Наш выбор логического подхода определяется достаточно быстрым получением реальных результатов для хорошо формализуемых задач.

Механизм вывода

· Замена дедукции на аргументацию. При обосновании решения основной операцией становится поиск аргументов, подтверждающих утверждение, которое система должна доказать или опровергнуть.

·        Сочетание достоверного (дедуктивного) и правдоподобного (индуктивного, по аналогии) вывода.

·        Способность системы по мере необходимости ослаблять или усиливать принятые в задаче допущения.

·        Присутствие немонотонных рассуждений: поступившие факты могут изменить истинность выведенных ранее заключений.

 

Минимаксный принцип

Поскольку полный просмотр игрового дерева в большинстве игр невозможен были разработаны другие методы, предусматривающие просмотр только части дерева игры. Среди этих методов существует стандартный метод поиска, используемый в игровых (особенно в шахматных) программах и основанный на минимаксном принципе. Дерево игры (И/ИЛИ-граф) просматривается только вплоть до некоторой глубины (обычно на несколько ходов), а затем для всех концевых вершин дерева поиска вычисляются оценки позиций при помощи некоторой оценочной функции. Идея состоит в том, чтобы, получив оценки этих терминальных поисковых вершин, не продвигаться дальше и получить тем самым экономию времени. Далее оценки терминальных позиций распространяются вверх по дереву поиска в соответствии с минимаксным принципом. В результате все вершины дерева поиска получают свои оценки. И, наконец, игровая программа, участвующая в некоторой реальной игре, делает свой ход - ход, ведущий из исходной (корневой) позиции в наиболее перспективного (с точки зрения оценки) ее преемника.

Обратите внимание на то, что мы здесь делаем определенное различие между "деревом игры" и "деревом поиска". Дерево поиска - это только часть дерева игры (его верхняя часть), т. е. та его часть, которая была явным способом порождена в процессе поиска. Таким образом, терминальные поисковые позиции совсем не обязательно должны совпадать с терминальными позициями самой игры.

Очень много зависит от оценочной функции, которая для большинства игр, представляющих интерес, является приближенной эвристической оценкой шансов на выигрыш одного из участников игры. Чем выше оценка, тем больше у него шансов выиграть и чем ниже оценка, тем больше шансов на выигрыш у его противника. Поскольку один из участников игры всегда стремиться к высоким оценкам, а другой - к низким, мы дадим им имена МАКС и МИН соответственно. МАКС всегда выбирает ход с максимальной оценкой; в противоположность ему МИН всегда выбирает ход с минимальной оценкой. Пользуясь этим принципом (минимаксным принципом) и зная значения оценок для всех вершин "подножья" дерева поиска, можно определить оценки всех остальных вершин дерева.
На рис. 2. 11 показано, как это делается. На этом рисунке видно, что уровни позиций с ходом МАКСа чередуются с уровнями позиций  с ходом МИНа. Оценки вершин нижнего уровня определяются при помощи оценочной функции. Оценки всех внутренних вершин можно определить, двигаясь снизу вверх от уровня к уровню, пока мы не достигнем корневой вершины. в результате, как видно на рис. 2.11, оценка корня оказывается равной 4, и, соответственно, лучшим ходом МАКСа из позиции a  -  a-b. Лучший ответ МИНа на этот ход - b-d, и т.д. Эту последовательность ходов называют также основным вариантом.  Основной вариант показывает, какова "минимаксно-оптимальная" игра для обоих участников. Обратите внимание на то, что оценки всех позиций, входящих в основной вариант совпадают.

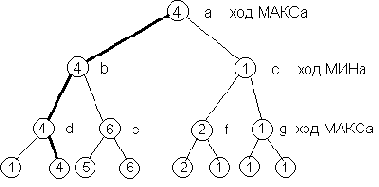Рис. 2.11. Статический (нижний уровень) и минимаксные рабочие

                      оценки вершин дерева поиска. Выделенные ходы образуют

                            основной вариант, т. е. минимаксно-оптимальную игру

                             с обеих сторон

Мы различаем два вида оценок: оценки вершин нижнего уровня и оценки внутренних вершин (рабочие оценки). Первые из них называют также "статическими", так как они вычисляются при помощи "статической" оценочной функции, в противоположность рабочим оценкам, получаемых "динамически" при распространении статических оценок вверх по дереву.

Правила распространения оценок можно сформулировать следующим образом. Будем обозначать статическую оценку позиции P через v(P), а ее рабочую оценку - через V(P). Пусть P1, P2, … Pn - разрешенные преемники позиции P. Тогда соотношения между статическими и рабочими оценками можно записать так:

V(P) = v(P)

если P - терминальная вершина позиции дерева поиска (n=0);

V(P) = V(Pi)

если P - позиция с ходом МАКСа;

V(P) = V(Pi)

если P - позиция с ходом МИНа.

Приведем упрощенную программу на Прологе, вычисляющую минимаксную рабочую оценку для некоторой заданной позиции.



% Минимаксная процедура: minimax(P,GP,V)

% P - позиция, V - ее минимаксная оценка;

% лучший ход из позиции P ведет в позицию GP

minimax(P,GP,V):-

      'ходы'(P,List),!,             % List - список разрешенных ходов

      'лучшая'(List,GP,V);

     'статическая оценка'(P,V).  % позиция P не имеет преемников

'лучшая'([P],P,V):-

     minimax(P,_,V),!.

'лучшая'([P1|List],GP,GV):-

     minimax(P1,_,V1),

     'лучшая'(List,P2,V2),

     'выбор'(P1,V1,P2,V2,GP,GV).

'выбор'(P0,V0,P1,V1,P0,V0):-

     'ход МИНа'(P0),V0>V1,!;

     'ход МАКСа'(P0),V0<V1,!.

'выбор'(P0,V0,P1,V1,P1,V1).

Основное отношение этой программы minimax(P,GP,V), где V - минимаксная оценка позиции P, а GP - наилучшая позиция-преемник позиции P ( лучший ход, позволяющий достигнуть оценки V). Предикат  'ходы'(P,List) задает разрешенные ходы игры: List - это список разрешенных позиций-преемников позиции P. Предполагается, что цель 'ходы' имеет неуспех, если P является терминальной поисковой вершиной (листом дерева поиска). Отношение 'лучшая'(List,GP,V) выбирает из списка позиций-кандидатов List "наилучшую" позицию GP. V - оценка позиции GP, а, следовательно, и позиции-предка. Под "наилучшей" оценкой мы понимаем либо максимальную, либо минимальную оценку, в зависимости от того, с чьей стороны ожидается ход.

Направления

·      Бионическое направление

Искусственное воспроизведение тех структур и процессов, которые характерны для живого человеческого мозга и которые лежат в основе процесса решения задач человеком. Это направление имеет четко выраженный фундаментальный характер, и его интенсивное развитие невозможно без одновременно глубокого изучения мозга нейрофизиологическими, морфологическими и психологическими методами.

·         Программно-прагматическое направление

Создание программ, с помощью которых можно было решать те задачи, решение которых до этого считалось исключительно прерогативой человека (распознающие программы, простейшие игровые программы, программы для решения логических задач, поиска, классификации и т. п.).

Основные методы поиска

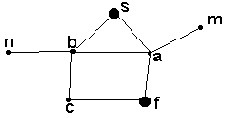Существует много различных подходов к проблеме поиска решающего пути для задач сформулированных в терминах пространства состояний. В качестве примера графа, представляющего пространство состояний некоторой задачи, мы будем использовать граф на рис. 2.3. Поскольку мы считаем, что по любому ребру мы можем двигаться в обоих направлениях, то стрелки на ребрах не указаны.

Рис. 2.3. Пространство состояний. s -начальная

 вершина, f - целевая вершина

При поиске пути из начальной в целевую вершину нам необходимо:

·        использовать некоторую схему учета, позволяющую упорядоченным способом исследовать все возможные пути;

·        не допускать циклов.

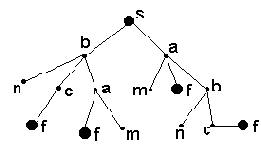Для лучшего представления множества путей в графе полезно будет преобразовать граф в дерево (рис. 2.4), при этом корнем дерева является начальная вершина, а листья дерева - это целевые или тупиковые вершины (тупики возникают в связи с нашим требованием не допускать циклов).

Рис. 2.4. Преобразование графа в дерево

Заметим, что число ярусов в полученном дереве не превосходит числа вершин в графе.

Особенности организации интенционального опыта

· Предпочтения

Большинство одаренных людей предпочитают иметь дело со сложными объектами и ситуациями (им больше нравятся дисгармонические геометрические фигуры, они выбирают для решения более неоднозначные и трудные задачи, их привлекают в первую очередь парадоксальные и противоречивые сведения и т.п.).  С другой стороны, интеллектуальные предпочтения уникальны, о чем свидетельствует крайнее разнообразие проявлений индивидуального интеллектуального выбора. По сути дела, предпочтения - это своего рода ментальный компас, выводящий человека в ту строго определенную область действительности, которая находится в максимальном соответствии с его индивидуальными интеллектуальными возможностями и в которой его интеллектуальные ресурсы могут реализоваться с максимальной эффективностью. В этом отношении прав был Дж. Пойа, когда писал, что "… логика - это дама, стоящая у выхода магазина самообслуживания и проверяющая стоимость каждого предмета в большой корзинке, содержимое которой отбиралась не ей".

·        Убеждения

1.  Вера в наличие определенных принципов, которым подчиняется природа изучаемых объектов.

2.  Изначальная уверенность в правильности выбранного пути изучения реальности.

"На том стою и не могу иначе" – чрезвычайная помехоустойчивость интеллектуального труда одаренных людей.

·        Умонастроение

Формируется особого рода "бессодержательное знание", благодаря которому такой человек заранее знает, что ему нужно и что ему не нужно делать.

Пойа: "Полезная идея всегда возникает вместе с ощущением     уверенности в том, что цель может быть достигнута и что именно данный элемент проблемной ситуации обязательно приведет к решению".

Особенности организации когнитивного опыта

Переработка информации происходит одновременно на трех уровнях:

· через знак (словесно-речевой способ кодирования информации);

·        через образ (визуально-пространственный);

·        через чувство (чувственно-сенсорный способ).

Когда мы нечто понимаем, мы это словесно определяем, мысленно видим и чувствуем.

Становление интеллекта предполагает развитие способности осуществлять обратимые переводы с одного "языка" на другой.

Особенности организации метакогнитивного опыта

В составе метакогнитивного опыта можно выделить четыре типа ментальных структур, обеспечивающих различные формы саморегуляции интеллектуальной активности: непроизвольный интеллектуальный контроль, произвольный интеллектуальный контроль, метакогнитивная осведомленность и открытая познавательная позиция.

·        Непроизвольный интеллектуальный контроль

     Когнитивные стили:

1.     "Узость – широта сканирования видимого поля". В данном случае речь идет об индивидуальных различиях в том, как организуется внимание человека при его столкновении с проблемной ситуацией.

2.     "Импульсивность-рефлективность". Подавление проявления импульсивности в ситуации принятия решений ("держать паузу") говорит не столько о том, что человек склонен более медленно перерабатывать информацию, сколько о тщательности и точности сбора информации до момента принятия решения.

3.     "Широта категории". Одни люди строят свои суждения о происходящем на основе использования широких категорий, ориентируясь на сходство объектов и явлений, другие - на основе использования узких категорий, обращая внимание в основном на отличительные черты тех же самых объектов и явлений.

4.     Особенности ориентировки в течение субъективного времени. Имеются в виду либо эффекты быстрого, либо медленного течения времени, а также эффекты хаотической ориентировки во времени. Психическое время течет более медленно у людей с низким уровнем структурированности психического пространства (с малым ментальным опытом).

·        Произвольный интеллектуальный контроль

Основными индикаторами сформировавшихся метакогнитивных структур опыта, лежащих в основе произвольного интеллектуального контроля, являются:

1.     Способность планировать - выдвигать цели и подцели собственной интеллектуальной деятельности, продумывать средства их реализации, выстраивать последовательность собственных действий и т.д.

2.     Способность предвосхищать - учитывать последствия принимаемых решений, а также прогнозировать возможные изменения проблемной ситуации. 2000 лет назад китайский философ Шан Ян охарактеризовал эту способность следующим образом: "Глупый не понимает сути дела, даже когда оно уже выполнено. Умный же постигает суть дела еще до того, как появятся первые его признаки".

3.     Способность оценивать – субъективно определять качество отдельных "шагов" собственной интеллектуальной деятельности ("Похоже, здесь я ошибся…"), ее результата ("Ай, да Пушкин! Сукин сын!"), а также собственных знаний в той или иной предметной области (в том числе и в такой экстремальной, доступной только мудрецам форме как "я знаю только то, что я не знаю").

4.     Способность прекращать или притормаживать интеллектуальную деятельность на любом этапе ее выполнения.

5.     Способность выбирать стратегию собственного обучения и модифицировать ее под влиянием новых требований и с учетом своих интеллектуальных способностей. Жизнь и другие люди, конечно, учат многому. Однако вопрос заключается в том, что эти уроки могут оказаться бесполезными, если они не сочетаются со способностью человека к произвольному самообучению.

·        Метакогнитивная осведомленность

Метакогнитивная осведомленность - это особая форма ментального опыта, характеризующая уровень и тип интроспективных (introspectare - лат. - смотреть внутрь) представлений человека о своих индивидуальных ресурсах. Метакогнитавная осведомленность предполагает:

1.     Знание своих индивидуальных интеллектуальных качеств (каковы особенности собственной памяти, мышления, предпочитаемые способы постановки и решения проблем и т.д.), а также  знание оснований своей интеллектуальной деятельности (в виде представлений о закономерностях запоминания, правилах эффективного мышления, различиях между логическими необходимыми и эмпирически верными суждениями и т.д.).



2.     Умение оценивать свои индивидуальные интеллектуальные качества как на уровне "плохой - хороший", " недостаточный - достаточный", так и на уровне самопринятия. Заметим, что чувство интеллектуальной состоятельности (либо интеллектуальной несостоятельности) может существеннейшим образом влиять на темп и характер интеллектуального развития личности.

3.     Готовность использовать приемы стимулирования и настройки работы своего собственного интеллекта. Соответственно, одним из критерием интеллектуальной зрелости является возможность человека оперативно и эффективно мобилизовать свои интеллектуальные силы для решения возникшей проблемы. Необходимо подчеркнуть, что приемы интеллектуальной самонастройки у каждого человека предельно индивидуализированы. Кому-то для того, чтобы привести себя в состояние пика интеллектуальной формы, надо принять горячую ванну, кому- то стать под холодный душ, кому-то включиться в бурную дискуссию, кому-то совершить одинокую прогулку и т.д. вплоть до самых экстравагантных способов произвольной мобилизации своих интеллектуальных сил.

·        Открытая познавательная позиция

О сформированности открытой познавательной позиции можно судить по ряду специфических состояний индивидуального ума:

1.     Осознание возможности множества разнообразных мысленных "взглядов" на одно и то же явление.

2.     Готовность использовать множество варьирующих способов описания и анализа того или иного явления. В том числе способность произвольно переходить от одного способа к другому (от логико-аналитического - к образному, от интуитивно-ассоциативного - к алгоритмическому, от действенно-практического - к игровому и т.д.).

3.     Осознание необходимости учета точки зрения другого человека, а также способность синтезировать разные познавательные позиции в условиях диалога с другими людьми.

4.     Особое отношение к парадоксам и противоречиям, связанное с готовностью принимать любые необычные сведения без каких-либо субъективных защитных искажений.

5.     Относительный характер индивидуальных суждений, проявляющийся в возможности, с одной стороны, соглашаться с явно различающимися по своему содержанию источниками информации и, с другой стороны, сомневаться в, казалось бы, очевидном и бесспорном источнике информации. Так известна притча о мудреце, к которому пришли для разрешения своего спора два человека. Внимательно выслушав прямо одного, мудрец заявил: "Ты прав, уважаемый!" После этого, столь же внимательно выслушав прямо противоположные аргументы другого, мудрец изрек:  "И ты прав, уважаемый!" Когда же жена мудреца, не вытерпев, отчитала мужа за столь нелепое поведение, он и ей ответствовал: "И ты права, дорогая!".

6.     Восприятие происходящего по принципу "возможно все – даже то, что невозможно". Обычно, чем человек умнее, тем труднее его чем-либо удивить: даже самые невероятные события оказываются для него  субъективно ожидаемые.

Перечислим некоторые вехи в развитии искусственного интеллекта

Перечислим некоторые вехи в развитии искусственного интеллекта в контексте других событий, связанных с ИИ. События, происшедшие в области ИИ отмечены звездочкой (*).

1637	Декарт: "Я мыслю, следовательно я существую."
1672-76	Лейбниц сформулировал в общих чертах подход к построению логического исчисления "machina ratiocinatrix"
1726	Джонатан Свифт в "Путешествиях Гулливера" описывает машину, которая пишет книги случайным образом.
1769*	Машина для шахматной игры В. фон Кемпелена, по-видимому, основана на обмане
1793*	Ф. Т. фон Шубертом предложен алгоритм разложения арифметических выражений на множители
1818	Шелли Мэри, английская писательница, в романе "Франкештейн, или Современный Прометей" пишет об искусственном создании, который уничтожает своего создателя.
1835	Джозеф Генри изобрел электрическое реле.
1847	Джордж Буль создал символическую логику, и позже двузначную логику.
1859	Чарльз Дарвин: "Происхождение видов путем естественного отбора".
1876	Александр Грейам Белл получает патент на телефон (US Patent 174,465).
1879	Томас Алва Эдисон изобретает лампочку.
1879	Готлоб Фреге изобретает исчисление предикатов.
1901	Зигмунд Фрейд: " Интерпретация снов".
1904	Первая вакуумная трубка, диод (John Ambrose Fleming).
1912*	Автомат для эндшпиля король и ладья против короля (Торрес-и-Квебедо Л.)
1913	Генри Форд вводит сборочный конвейер.
1915	Общая теория относительности Эйнштейна
1917*	Карел Чапек вводит термин "робот" (в чешском языке "робот" означает "рабочий", но в 1923 году английский перевод оставляет оригинальное слово)
1925	Р. Вагнер обнаружил наличие обратной связи в биологических системах
1928*	Джон фон Нейман доказал теорему о минимаксе (позднее использовалась в программах для теории игр).
1931	Теорема Геделя о неполноте.
1936	Общественное телевидение в Великобритании
1937	Алан Тьюринг публикует "On Computable Numbers", где он вводит "машину Тьюринга" - формализация понятия алгоритма.
1940	Atanasoff и Berry создают первый электронный компьютер.
1940	Robinson – первый действующий компьютер в Великобритании, базирующийся на реле; использовался, чтобы декодировать нацистские коды
1940	Первая цветная телевизионная передача
1941	Конрад Цузе создает в Германии Z3 - первый программируемый компьютер
1943*	У. Макколлак (McCulloch) и У. Питц (Pitts) предлагают формальную модель, отражающую функционирование нейрона; начало нейрокибернетики.
1944	Х. Х. Айкен завершает 'Mark I', первый американский программируемый компьютер
1945	Grace Murray Hopper обнаруживает при работе вычислительной машины первого "жучка" ("bug")  (9-09-45 15:45 - запись в журнале)
1946	Джон фон Нейман предлагает логическую конструкцию электронной вычислительной машины с программой, хранимой в памяти.
1947	Основывается ACM (Association for Computing Machinery)
1948	Норберт Винер: "Кибернетика, или Управление и связь в животном и машине" - начало кибернетики.
1949	Моррис Уилкс (Wilkes) создал EDSAC - первый компьютер с хранимой программой.
1949	К. Шеннон создает теорию информации.
1950*	Айзек Азимов: "Я - Робот"
1950*	Алан Тьюринг предложил "тест Тьюринга" - критерий на наличие интеллекта у искусственного создания.
1950	Дж. П. Эккерт (Eckert) и Дж. У. Мочли (Mauchley) продают UNIVAC – первый коммерческий компьютер.
1950	Программа текстового редактирования для машины EDVAS
1951	Бюро Переписи Населения (США) покупает Remington-Rand UNIVAC за $159,000 (позже $250,000).
1951	Трансконтинентальный черно-белый ТВ в США.
1953	Уотсон и Крик открывают химическую структуру ДНК
1953*	Х. Г. Кахриманян и Дж. Ф. Ноулан написали первые программы для машинного выполнения дифференцирования
1954*	Айзек Азимов: "Стальные пещеры"
1954	Смерть Тьюринга
1954*	А. Ньюэлл, Дж. Шоу и Г. Саймон разрабатывают "IPL-11" - первый язык ИИ
1954*	Работы по автоматическому переводу ведутся во многих странах – США, Советском Союзе, Израиле, Англии и др.
1955	IBM производит первый транзисторный калькулятор
1956*	А. Ньюэлл, Дж. Шоу и Г. Саймон создают программу "Логик-теоретик" ("The Logic Theorist"), которая сумела заново передоказать многие теоремы математической логики.
1956*	Первая конференция по ИИ в Джорджтаунском колледже;  встреча  А. Ньюэлла, Г. Саймона, Дж. Маккарти и М. Минского
1956	FORTRAN изобретен в IBM (Дж. Бэкус)
1956*	С. Улам разрабатывает "MANIAC I" - первую шахматную программу, которая победит человека
1957*	А. Ньюэлл, Дж. Шоу и Г. Саймон создают  General Problem Solver (GPS); программа основана на психологической теории решения задач человеком путем целесообразного выбора на множестве альтернатив.
1957	Хомский (N. Chomsky): "Синтаксические Структуры".
1958*	Джон Маккарти  изобретает Лисп в MIT.
1958	Создан язык ALGOL 58 .
1958	Jack St. Clair Kilby изобретает интегральную схему
1958*	Эвристические правила для доказательства геометрических теорем (Х. Гелернтер и Н. Рочестер)
1958*	М. Минский и Дж. Маккарти основывают MIT AI Lab
1959*	Эвристические правила для доказательства теорем исчисления предикатов первого порядка  (П. К. Гилмор)
1959*	Ф. Розенблатт вводит понятие "персептрон" - формальную модель распознавания, опирающую на использование формальных нейронов
1959*	Программа для игры в шашки (А. Сэмюэль - Samuel) выигрывает игры против лучших игроков-людей
1959	Robert Noyce независимо от Kilby изобретает интегральную схему.
1960*	Первые программы автоматического переноса при редактировании текста
1961*	Эвристические приемы формульного интегрирования (Дж. Р. Слэгл)
1962*	Первые коммерческие промышленные роботы.
1962	Томас Кун: "Структуры научных революций".
1962	Карло Хинтикка: "Знания и убеждения".
1962	Сол Крипке "Семантика возможных миров".
1963*	M. Ross Quillian (Семантические сети - как представление знания)
1963*	М. Минский "Шаги по направлению к искусственному интеллекту"
1964	IBM вводит 360 серию
1964	Языки программирования PL/1, BASIC
1965*	Метод резолюций в логическом программировании (Дж. А. Робинсон)
1965	Язык программирования APL
1965*	Buchanan, Feigenbaum и Lederberg начинают проект экспертной системы "ДЕНДРАЛ" (самая известная впоследствии)
1965*	Г. Саймон предсказывается "В 1985-м машины будут способны сделать любую работу, которую может делать человек"
1965*	Х. Дрейфус (Hubert Dreyfus) спорит против возможности искусственного интеллекта
1966*	Знаменитая программа Вейценбаума ( Weizenbaum) ELIZA, имитирующая беседу психоаналитика с пациентом
1967*	MacHack побеждает Дрейфуса в шахматы
1968*	Письмо Э. В. Дейкстры в  CACM "GO TO statement considered harmful" – против использования оператора перехода.
1968*	Chomsky и Halle: "The Sound Pattern of English"
1969	John McCarthy и Pat Hayes "Философские проблемы с точки зрения искусственного интеллекта" (Исчисление ситуаций).
1969	Alan Kay в своей докторской диссертации описывает теоретически персональный компьютер.
1969	Кнут Д. "Искусство программирования для ЭВМ" том. 1
1969	UNIX (Thomson и Ritchie в AT&T)
1970*	Prolog (Колмероэ - Colmerauer)
1970	Флоппи-дискеты
1970*	Программа Терри Винограда  (Winograd Terry) SHRDLU (Обработка Естественного Языка, Мир Блоков)
1971	Первый микропроцессор в США (Intel 8008)
1971	Первый карманный калькулятор (Poketronic)
1971	Паскаль (Н. Вирт)
1972*	Х. Дрейфус: "Чего не могут вычислительные машины"
1972*	Язык Смолток (Smalltalk) разработан в Xerox PARC (Kay)
1972	Cray Research
1973*	Schank и Abelson вводят понятие скрипт (сценарий) - один из методов представления знаний.
1974*	Первый управляемый робот
1974*	М. Минский: "A Framework for Representing Knowledge" - фреймы для представления знаний.
1975*	Cooper и Erlbaum основывают Nestor, чтобы разработать технологию нейронных сетей.
1975	Первый персональный компьютер Altair 8800 (256 байт памяти)
1976*	Greenblatt создает первую Лисп-машину "CONS"
1976*	Kurzweil создает читающую машину
1976	Cray-1 – супер-компьютер, 138 мегафлоп
1977	Wozniak и Jobs разрабатывают Apple Computer
1977	Основан Microsoft
1978	Экспертная система SRI's PROSPECTOR обнаруживает молибденовую жилу
1978*	Основание Xerox LISP machines
1979*	Raj Reddy основывает Институт Робототехники в Carnegie Mellon University
1979*	MYCIN – медицинский эксперт (экспертная система описана в Журнале Американской Медицинской Ассоциации.)
1980*	Экспертные системы вплоть до тысячи правил
1980*	Hofstadter написал "Гедель, Эшер, Бах"
1980	Xerox, DEC и Intel вводят Ethernet
1981	А. Ньюэлл: "The Knowledge Level"
1981	IBM выпускает  персональный компьютер (PC)
1981*	Японский Проект Эвм Пятого Поколения
1981*	PSL (Портативный Стандартный Лисп) работающий на целом ряде платформ
1981*	ЛИСП-машины от Xerox, LMI, и Symbolics доступные коммерчески, делают динамическую OOP технологию широко доступной
1981*	Определяется Common Lisp - фактический стандарт на язык Лисп
1982*	Джон Хопфилд (Hopfield) "оживляет" нейронные сети
1982*	Экпертная система SRI's PROSPECTOR обнаруживает основной депозит молибдена
1982	IBM PC
1983*	Айзек Азимов пишет "Robots of Dawn"
1983	IBM вводит PCjr
1983	Sony заявляет о технологии CD
1983	С. Лем предсказывает появление компьютерных вирусов в романе "Мир на Земле"
1984-86	Корпорации инвестируют 50 миллион $ на разработку ИИ
1984*	Gold Hill создает Golden Common LISP
1984*	"Wabot-2" читает музыку с листа и играет на органе
1984	Apple создает Macintosh
1984	Изобретены оптические диски
1985*	GM и Campbell's Soup не используют Лисп для экспертных систем
1985*	Робот Kawasaki убивает японского механика в результате сбоя
1985*	М. Минский публикует "The Society of Mind"
1985*	Teknowledge отказывается от Лиспа и Пролога в пользу C
1985	C++
1986*	Промышленный доход ИИ теперь $1,000,000,000
1986*	Робот-игрок (Anderson) обыгрывает в пинг-понг человека
1986*	Borland предлагает Turbo PROLOG за $99
1986*	Полиция Далласа использует робота чтобы прорваться в квартиру
1986*	Первая OOPSLA конференция по объектно-ориентированному программированию, в котором CLOS впервые рекламируется за пределами Lisp/AI общества
1986*	McClelland и Rumelhart: "Parallel Distributed Processing" (Нейронные Сети)
1987*	1,900 работающих экспертных систем
1987*	Доход ИИ - 1.4 миллиарда $, исключая робототехнику
1987*	Экспертная система "XCON" фирмы DEC, используемая для конфигурации компьютеров, делают работу 300 людей, применяя 10,000 правил
1987	Япония разрабатывает Систему Автоматизированной Идентификации Отпечатка Пальца
1988*	386 чип приводит PC к скорости конкурирующей с машинами LISP
1988*	Доход экспертных систем - более 400 миллионов $
1988*	Hillis "Connection Machine" способна выполнять 65,536 параллельных вычислений
1988*	М. Минский и Пайперт (Papert) опубликовали дополненное и исправленное издание "Perceptrons"
1988*	Объектно-ориентированные языки
1988	Червь Морриса: сетевой вирус
1988	Система Mathematica 1.0 (С. Вольфрам)
1990	Новые PC, NeXT, Mac SUN, DEC
1992*	Apple Computer вводит Dylan, язык из семейства Lisp, как предтечу для будущих языков
1992	Закончен Японский Проект Эвм Пятого Поколения
1992	Начало японского проекта Real World Computing
1992	Более чем 1000 типов компьютерных вирусов

Подходы

1. Локальный или “задачный” - основан на точке зрения, что для каждой задачи, присущей творческой деятельности человека, можно найти способ ее решения на ЭВМ, который будучи реализован в виде программы, дает результат, либо подобный результату полученному человеком, либо даже лучший.

2. Системный или основанный на знаниях связан с представлением о том, что решение отдельных творческих задач не исчерпывает всей проблематики искусственного интеллекта. Естественный интеллект человека способен не только решать творческие задачи, но и при необходимости обучается тому или иному виду творческой деятельности. Поэтому и программы искусственного интеллекта должны быть ориентированны не только или не столько на решение конкретных интеллектуальных задач, сколько на создание средств, позволяющих автоматически строить программы решения интеллектуальных задач, когда в таких программах возникнет необходимость.

3. Подход рассматривает проблемы создания интеллектуальных систем как часть общей теории программирования (как некоторый новый виток в этой теории). При этом подходе для составления интеллектуальных программ используются обычные программные средства, позволяющие писать нужные программы по описаниям задач на профессиональном естественном языке. Все метасредства, возникающие при этом на базе частичного анализа естественного интеллекта, рассматриваются здесь лишь с точки зрения создания интеллектуального программного обеспечения, т. е. комплекса средств, автоматизирующих деятельность самого программиста.

Поиск в глубину

Поиск в глубину основывается на следующей стратегии:

В каждой вершине выбирается какая-то определенная альтернатива, и ее изучение продолжается до тех пор, пока дальнейшее продвижение оказывается невозможным. Тогда процесс поиска возобновляется от ближайшей точки ветвления, имеющей неисследованные альтернативные варианты.

Поиск в глубину основывается на предположении "любой данный путь хорош, как и всякий другой". На рис. 2.5 показан порядок обхода вершин при поиске в глубину.

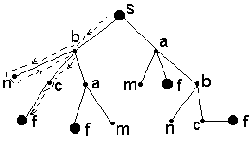Рис. 2.5. Поиск в глубину

Поиск в глубину обладает следующими недостатками: а) во-первых, отыскивается не самый короткий путь; б) во-вторых, если в дереве есть бесконечные ветви и если такая бесконечная ветвь встретится - поиск никогда не закончится, даже если есть конечный путь в целевую вершину.

 Поиск в глубину легко запрограммировать на Прологе.

% поиск в глубину

solve(Start,Solve):-            % Start - начальная вершина, Solve - искомый путь

         depth([],Start,Solve).

        

 depth(P,X,[X|P]):-

               goal(X).      % этот предикат проверяет, является ли вершина целевой

         

   depth(P,X,Solve):-

          next(X,X1),           

          not(member(X1,P)),

          depth([X|P],X1,Solve).

Предикат depth использует первый аргумент для накопления пройденного пути. Вершины в пути перечисляются в обратном порядке.

Для графа на рис. 2.3 мы можем экономно определить отношение next:

'ребра'([[s,b],[s,a],[b,n],[b,c],[c,f],[a,m],[a,f],[a,b]]).

next(X,Y):-

      'ребра'(L),

      (member([X,Y],L);member([Y,X],L)).

Добавим также к программе факт goal(f). Тогда имеем:

?- solve(s,X).

X = [f, c, b, s] ;

X = [f, a, b, s] ;

X = [f, a, s] ;

X = [f, c, b, a, s] ;

No

Вернемся к задаче о перестановке кубиков. Добавим предикат printList для удобной печати списка и предикат run для простоты запуска программы.

printList([]).

printList([H|T]):-

        write(H),nl,

        printList(T).

run:-

   solve([[c,a,b],[],[]],Solve),

   printList(Solve).

goal(S):- member([a,b,c],S).

Решим задачу:

?- run.

[[], [a, b, c], []]

[[a], [b, c], []]

[[b, a], [c], []]

[[], [c, b, a], []]

[[c], [b, a], []]

[[], [b, c], [a]]

[[b], [c], [a]]

[[], [c, b], [a]]

[[a], [c], [b]]

[[], [c, a], [b]]

[[c], [a], [b]]

[[], [a, c], [b]]

[[a], [b], [c]]

[[], [b, a], [c]]

[[b], [a], [c]]

[[], [c], [a, b]]

[[], [c], [a, b]]

[[c], [a, b], []]

[[a, c], [b], []]

[[], [b, a, c], []]

[[b], [a, c], []]

[[a, b], [c], []]

[[c, a, b], [], []]

Yes

У нас получилось поистине "ужасное" решение. Разберемся в чем причина. Во-первых, ситуации в найденном решении повторяются: например, состояния [[], [c], [b,a]], [[c], [b,a], []] и [[b,a], [c], []] в программе различаются. Это явилось следствием того, что в списке столбиков учитывается порядок. Для улучшения программы надо столбики рассматривать как элементы множества и заменить предикат member более сложным предикатом. Во-вторых, в решения встречаются два одинаковых состояния, идущих подряд

[[], [c], [a, b]]

[[], [c], [a, b]]

Это уже следствие недостаточно хорошего определения предиката next. Дело в том, что одним из состояний-преемников для [[], [c], [a, b]]  является состояние [[c], [], [a, b]], которое предикат next выдает в виде [[], [c], [a, b]]. Здесь снова при программировании next надо учесть, что порядок перечисления столбиков в состоянии для нас не важен.

Если известна верхняя граница длины решающего пути, то можно ограничить глубину поиска.

% Поиск в глубину с ограничением глубины

solve(Start,Solve):-            % Start - начальная вершина, Solve - искомый путь

         depth([],Start,Solve).

depth(P,X,[X|P]):-

       goal(X),

       length([X|P],N),nl, 

       write('Нашли решение за '),write(N),write(' шагов '),nl.

depth(P,X,Solve):-

       maxlength(Max),

       length(P,N),

       N+1<Max,

       next(X,X1),

       not(member(X1,P)),

       depth([X|P],X1,Solve).

% maxlength(N) -> N - максимальная глубина;

maxlength(10).

 Теперь, чтобы решить задачу (при поиске в глубину с ограничением 10) достаточно запустить цель

?- run.

Нашли решение за 10 шагов

[[], [a, b, c], []]

[[], [b, c], [a]]

[[b], [a], [c]]

[[], [c], [a, b]]

[[c], [a, b], []]

[[a, c], [b], []]

[[], [b, a, c], []]

[[b], [a, c], []]

[[a, b], [c], []]

[[c, a, b], [], []]

Yes

Поиск в глубину наиболее адекватен рекурсивному стилю программирования, принятому в Прологе. Причина этого состоит в том, что, обрабатывая цели, пролог-система сама просматривает альтернативы именно в глубину.

Поиск в И/ИЛИ-графах

Простейший способ организовать поиск в И/ИЛИ-графах средствами Пролога - это использовать переборный механизм, заложенной в самой пролог-системе. Оказывается, что это очень просто сделать, потому что процедурная семантика Пролога это и есть не что иное, как поиск в И/ИЛИ-графе. Например, И/ИЛИ-граф задачи на рис. 2.7 можно описать при помощи следующих предложений (предикат a-z соответствует задаче "найти путь из a в z", предикат a-z/f соответствует задаче "найти путь из a в z через f" и т.д.):

a-z:-a-z/f.        % задача a-z - ИЛИ-вершина с двумя преемниками

a-z:-a-z/g.       % a-z через f и a-z через g

a-z/f:- a-f,f-z.  % задача a-z/f - И-вершина с двумя преемниками a-f и f-z

a-z/g:-a-g,g-z.

a-f:-a-f/b.

a-f:-a-f/c.

a-f/b:-a-b,b-f.

a-f/c:-a-c,c-f.

b-f:-b-d,d-f.

c-f:-c-e,e-f.

f-z:-f-z/h.

f-z:-f-z/i.

f-z/h:-f-h,h-z.

f-z/i:-f-i,i-z.

/* пропущены правила

   для a-g и g-z

*/

a-b. b-d. d-f. a-c. c-e. e-f. f-h. h-z. f-i. i-z. % "тривиальные" задачи

 

Для того чтобы узнать, имеет ли эта задача решение, нужно просто спросить:

?- a-z.

Получив этот вопрос, пролог-система произведет поиск в глубину в И/ИЛИ-дереве и, после того как найдет решающее дерево, ответит Yes.

За простоту такого метода программирования приходится расплачиваться: мы не получаем явно решающего дерева. Но этот недостаток исправим - надо определить собственную процедуру поиска в глубину для И/ИЛИ-дерева.

Поиск в ширину

При поиске в ширину целевая вершина сначала отыскивается среди всех вершин, расположенных на данном уровне, прежде чем будут исследованы ветви, отходящие вниз от этих вершин (рис. 2.6). Иными словами, сначала ищем решение среди путей длины один, потом - длины два и т.д.

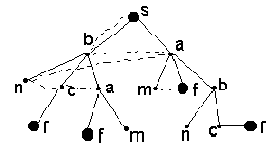Рис. 2.6. Поиск в ширину

Очевидно, что этот поиск применим, даже если дерево бесконечно или практически бесконечно. К недостаткам этого поиска можно отнести неэффективность: если b - среднее число альтернатив для каждой внутренней вершины, то число путей длины n равно в среднем bn.

Поиск в ширину программируется на Прологе немного сложнее.

% поиск в ширину

solve(Start,Solve):-

        width([[Start]],Solve).

       

width([[X|P]|_],[X|P]):- goal(X).    

width(Ps,Solve):-

           gener(Ps,Npath),

           width(Npath,Solve).

newPath([],_,[]).

newPath([X|T],L,[[X|L]|LL]):-

            newPath(T,L,LL).

postList(X,L,K):-

      findall(Y, (next(X,Y),not member(Y,L)),K).

          

gener([[X|L]|T],Npath):-

              postList(X,L,K),      

              newPath(K,[X|L],ZZ),

              append(T,ZZ,Npath).

Предикат width(LL,S) использует аргумент LL для хранения всех начатых и еще не рассмотренных путей. LL представляет из себя список путей - список списков. Рассматриваемый в текущий момент путь является головой списка LL. Если этот путь приходит в целевую вершину, то решение найдено (это первое правило для width). Иначе применяется второе правило для width: создается новый список путей - кандидатов к рассмотрению - и рекурсивно вызывается снова width.

Предикат gener([[X|L]|T],Npath) удлиняет на одну вершину первый путь [X|L] из списка путей-кандидатов и множество удлиненных путей добавляется в конец списка путей-кандидатов. Используемый в нем вызов предиката postList(X,L,K) создает список K вершин-преемников вершины X, не принадлежащих списку L.

Проверим, как работает программа. Сначала поиск в ширину в графе на рис. 2.3:

?- solve(s,Solve).

Solve = [f, a, s] ;

Solve = [f, c, b, s] ;

Solve = [f, a, b, s] ;

Solve = [f, c, b, a, s] ;

No

Для задачи о кубиках поиск в ширину сразу выдает самое короткое решение:

?- run.

[[], [a, b, c], []]

[[], [b, c], [a]]

[[b], [a], [c]]

[[a, b], [c], []]

[[c, a, b], [], []]

Yes

Поиск в глубину и поиск в ширину относятся к стратегиям полного перебора. Эффективность поиска повышается, если упорядочить ветви, идущие от каждой вершины, - в первую очередь при переборе выбирать наиболее перспективные ветви. Мы используем это, скажем, при подъеме в гору, выбираем тропинки, идущие вверх. Другой пример: если вам надо на автомобиле пересечь незнакомый город в направлении с севера на юг, то вы предпочитаете ехать по широким улицам, идущим близко к этому направлению. Такая стратегия называется стратегией наискорейшего подъема (спуска).

Если мы отказываемся от полного перебора и отбрасываем некоторые, на наш взгляд, неперспективные ветви, то такой поиск называется эвристическим. Эвристический поиск быстрее находит решение, хотя и может быть неудачным. Пример: если мы должны выйти из леса в город, то следует предпочесть асфальтированные дороги проселочным.

Предмет "Искусственный интеллект"

Типичное изучение математики (как и любой формальной теории) в школе, в вузе сопровождается ощущением растерянности, недоумения. Определения и доказательства преподносят как настоящую реальность, но причины явлений никогда не объясняются. Казалось, что большую часть доказательств преподаватели получают с помощью магических манипуляций с кусочком мела у доски. Как можно было связать воедино все эти линии и не выпустить из поля зрения ни одну из них от самого начала доказательства до его чудесного конца? И над всем этим: "А для чего все это надо?".

Ответ приходит через несколько лет активной жизни. На самом деле все это ни для чего не надо, потому что предметы, которые вы изучаете, вносятся в школьные и вузовские программы достаточно произвольно. По правде говоря, эти знания служат лишь поводом для перехода к более серьезным вещам, таким как учиться понимать, учиться решать задачи, учиться познавать. Но любопытно, что эти "вещи" не признаются и не преподаются. Можно сказать, что существует определенный вид интеллектуального терроризма, когда некоторых учеников называют "нуль в математике", хотя их единственная вина состоит в том, что они не понимают то, о чем … никогда не говорится. Некоторым удается это избежать, потому что они раньше сумели познакомиться с неявными правилами этой игры. Есть и такие, кто учит все наизусть…

Но существует область исследований, в которой первым желанием исследователей является стремление понять, как система обработки информации - будь то человек или машина - способна воспринимать, анализировать, передавать и обобщать то, чему ее обучают и с помощью этих данных исследовать конкретные ситуации и решать задачи.

Данная область исследования – искусственный интеллект (artificial intelligence) – старший сын информатики.

Предмет исследования ИИ – любая интеллектуальная деятельность человека, подчиняющая заранее неизвестным законам. Его можно также определить как "все то, что еще не сделано в информатике"

Искусственный интеллект - это область исследований, находящаяся на стыке наук; специалисты, работающие в этой области, пытаются понять, какое поведение, считается разумным (анализ), и создать работающие модели этого поведения (синтез). Исследователи ставят вопрос с помощью новых теорий и моделей научиться понимать принципы и механизмы интеллектуальной деятельности. Практической целью является создание методов и техники, необходимой для программирования "разумности" и ее передачи компьютерам, а через них всевозможным системам и средствам. Инженерные методы и навыки в области ИИ стали называть технологией знаний (knowledge engineering).

В области ИИ у нас имеются трудности  двух типов:

1.     В большинстве случаев, выполняя какие-то действия, мы сами не осознаем, как мы это делаем – отсутствует алгоритм.

2.     Компьютеры априори далеки от человеческого уровня компетенции. До начала работы необходимо составить соответствующую программу. Но языки программирования позволяют выразить только элементарные понятия.

По своим методам ИИ – экспериментальная научная дисциплина.

Эксперимент  в ИИ - это проверка и уточнение моделей (компьютерных программ) на многочисленных примерах – наблюдениях над человеком с целью раскрыть эти модели и лучше понять функционирования человеческого разума.

Есть и новые мнения. Станислав Лем предложил (1997):

"ИИ должен стать своего рода экспериментальной философией. Только таким образом  удастся, наконец, совместить философские построения, основывающиеся на некоторых достаточно общих допущениях, и реальные выводы из той или иной философской системы. Сама эта система таким образом будет верифицирована, причем без вреда для цивилизации"

Впервые после фундаментального пересмотра картины мира (Коперник, Дарвин), разработка методов ИИ возвращает нас к вопросу о месте человека в природе. По существу впервые оспаривается исключительность разума.

Исследования в области ИИ рекурсивны - так как мы с помощью своего мышления пытаемся понять как мы мыслим.



Уточнение определения области ИИ.

Всякая задача, для которой неизвестен алгоритм решения, априорно относится к ИИ.

К сфере ИИ относятся все те различные области, где мы действуем не имея абсолютно точного метода решения проблемы.

Две характерные особенности:

·        В них используется информация в символьной форме: буквы, слова, знаки, рисунки.

·        Предполагается наличие выбора:

Ø     нет алгоритма = нужно сделать выбор между многими вариантами в условиях неопределенности;

Ø     недетерминизм, свобода действия – существенная составляющая интеллекта.

Если в численных вычислениях внимание уделяется количественной стороне и численным значениям данных, то в символьных вычислениях важна качественная сторона данных: особенности их строения и их функциональные особенности.

Поскольку ИИ имеет дело с символьной обработкой, то полезны специальные языки. Два широко распространенных языка в этой области Лисп и Пролог. Мы будем использовать в качестве инструмента для задач ИИ язык SWI-prolog.

Представление задач в виде И/ИЛИ-графов

Мы рассмотрели подход к решению задач, основанный на поиске пути в графе пространства состояний. Однако для некоторых категорий задач представление в форме И/ИЛИ-графа является более естественным. Такое представление основано на разбиении задач на подзадачи. Разбиение на подзадачи дает преимущества в том случае, когда подзадачи взаимно независимы, а, следовательно, и решать их можно независимо друг от друга.

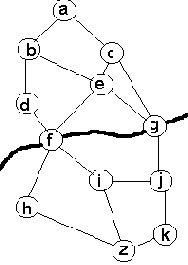Рис. 2.7. Поиск маршрута из a в z на карте дорог.

Через реку можно переправиться в городах f и g.

И/ИЛИ-представление этой задачи показано на рис. 2.8.

Проиллюстрируем это на примере. Рассмотрим задачу отыскания на карте дорог маршрута между двумя заданными городами, как показано на рис. 2.7.  Не будем учитывать длину путей. Разумеется, эту задачу можно сформулировать как поиск пути в пространстве состояний. Соответствующее пространство состояний выглядело бы в точности, как карта рис. 2.7: вершины соответствуют городам, дуги - непосредственным связям между городами. Тем не менее, давайте построим другое представление, основанное на естественном разбиении этой задачи на подзадачи. На карте рис. 2.7 мы видим также реку. Допустим, что переправиться через нее можно только по двум мостам: один расположен в городе f, другой - в городе g. Очевидно, что искомый маршрут обязательно должен проходить через один из мостов, а значит, он должен пройти либо через f, либо через g. Таким образом, мы имеем две главных альтернативы:

Для того чтобы найти путь из a в z, необходимо найти одно из двух:

(1) путь из a в z, проходящий через f, или

(2) путь из a в z, проходящий через g.

Теперь каждую из этих двух альтернативных задач можно, в свою очередь, разбить следующим образом:

(1) Для того, чтобы найти путь из a в z через f, необходимо:

1.1 найти путь из a в f и

1.2 найти путь из f в z.

(2) Для того, чтобы найти путь из a в z через g, необходимо:

2.1 найти путь из a в g и

2.2. найти путь из g в z.

Итак, мы имеем две главные альтернативы для решения исходной задачи: (1) путь через f или (2) путь через g.
Далее, каждую из этих альтернатив можно разбить на подзадачи (1.1 и 1.2 или 2.1 и 2.2 соответственно). Здесь важно то обстоятельство, что каждую из подзадач в обеих альтернативах можно решать независимо от другой. Полученное разбиение исходной задачи можно изобразить в форме И/ИЛИ -графа (рис. 2.8).

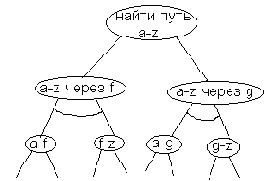Рис. 2.8. И/ИЛИ-представление задачи поиска маршрута рис.2.7

Вершины соответствуют задачам или подзадачам, полукруглые дуги означают, что все (точнее, обе) подзадачи должны быть решены.

Обратите внимание на полукруглые дуги, которые указывают на отношение И между соответствующими подзадачами. Граф, показанный на      рис. 2.8 - это всего лишь верхняя часть всего И/ИЛИ-дерева. Дальнейшее разбиение подзадач можно было бы строить на основе введения дополнительных промежуточных городов.

Какие вершины И/ИЛИ-графа являются целевыми? Целевые вершины - это тривиальные, или "примитивные" задачи. В нашем примере такой подзадачей можно было бы считать подзадачу "найти путь из a в c", поскольку между городами a и c на карте имеется непосредственная связь.

Рассматривая наш пример, мы ввели ряд важных понятий. И/ИЛИ-граф - это направленный граф, вершины которого соответствуют задачам, а дуги отношениям между задачами. Между дугами также существуют свои отношения. Это отношения И и ИЛИ, в зависимости от того, должны ли мы решить только одну из задач-преемников или же несколько из них (рис. 2.9). В принципе из вершины могут выходить дуги, находящиеся в отношении И вместе с дугами, находящимися в отношении ИЛИ. Тем не менее, мы будем предполагать, что каждая вершина имеет либо только И-преемников, либо только ИЛИ-преемников; дело в том, что в такую форму можно преобразовать любой И/ИЛИ-граф, вводя в него при необходимости вспомогательные ИЛИ-вершины. Вершину, из которой выходят только И-дуги, называют        И-вершиной; вершину, из которой выходят только ИЛИ-дуги, -                 ИЛИ-вершиной.



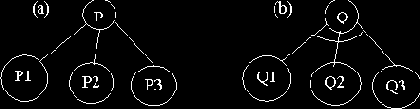Рис. 2.9. (a) Решить P - это значит решить P1или P2 или …

(b) Решить Q - это значит решить Q1 и Q2 и … .

Когда задача представлялась в форме пространства состояний, ее решением был путь в этом пространстве. Что является решением в случае И/ИЛИ-представления? Решение, конечно, должно включать в себя все подзадачи И-вершины. Следовательно, это уже не путь, а дерево. Такое решающее дерево T определяется следующим образом:

·        исходная задача P - корень дерева T;

·        если P является ИЛИ-вершиной, то в T содержится только один из ее преемников (из И/ИЛИ-графа) вместе со своим собственным решающим деревом;

·        если P - это И-вершина, то все ее преемники (из И/ИЛИ-графа) вместе со своими решающими деревьями содержатся в T.

Представление знаний

·        Используются не поверхностные знания, а глубинные, представляющие собой теории предметных областей (аналогичные естественнонаучным теориям) и общие стратегии решения проблем. Когда появляется новая проблема, экспертная система определяет конкретные знания, которые необходимо привлечь для решения.

·        Система имеет не только модель предметной области, но и модель самой себя (определяет границы своей компетентности - "знаю, что я это знаю").

·        Система включает средства для одновременной работы с несколькими моделями предметной области.

·        Имеется база знаний с неполной информацией.

Представление знаний и вывод знаний

Представление - это действие, делающее некоторое понятие воспринимаемым посредством рисунка, записи, языка или формализма. Теория знаний исследует связи между субъектом (изучающим) и объектом. Знание (в объективном смысле) - то, что известно (то, что мы знаем после изучения), т. е. - это совокупность сведений, образующих целостное описание, соответствующее некоторому уровню осведомленности об описываемом вопросе, предмете, проблеме и т.д.

Представление знаний - формализация знаний посредством фигур, записей или языков. Нас интересует формализации, воспринимаемые (распознаваемые) ЭВМ. Возникает вопрос о представлении знаний в памяти компьютера, т. е. о создании языков и формализмов представления знаний. Языки ИИ преобразуют наглядное представление (созданное посредством речи, изображением, естественным языком, вроде русского или английского, формальным языком, вроде алгебры или логики и т.д.) в пригодное для ввода и обработки на компьютере.

Представлению знаний присущ пассивный аспект: книга, таблица, заполненная информацией память. В ИИ подчеркивается активный аспект представления: знать должно стать активной операцией, позволяющей не только запоминать, но и извлекать воспринятые (приобретенные, усвоенные) знания (точнее, знания, которые запомнились) для рассуждения на их основе. 

Наиболее часто знания подразделяются на декларативные и процедурные. Процедурные знания - это знания, хранящиеся в памяти интеллектуальной системы в виде описаний процедур, с помощью которых их можно получить. В виде процедурных знаний обычно описываются информация о предметной области, характеризующая способы решения задач в этой области, а также различные инструкции, методики, алгоритмы. 

Знания декларативные - это знания, которые записаны в памяти интеллектуальной системы так, что они непосредственно доступны для использования после обращения к соответствующему полю памяти. В виде декларативных знаний обычно записывается информация о свойствах предметной области, фактах, имеющих в ней место, и тому подобная информация. В отличие от процедурных знаний, отвечающих на вопрос "Как сделать X?", декларативные знания отвечают, скорее, на вопросы: "Что есть X?" или "Какие связи имеются между X и Y?", "Почему X?" и т.д.

На концептуальном уровне представления знаний наиболее распространены модели знаний в виде семантических сетей, фреймов и продукционных систем.

Приобретение знаний и обучение

·        Имеются средства управления процессом наполнения экспертной системы знаниями и настройки на предметную область, позволяющие выбирать модель представления знаний, в наибольшей степени соответствующую структуре знаний эксперта.

·        Автоматическое обнаружение закономерностей в знаниях. Экспертная система  получает знания от эксперта и самостоятельно извлекает их из базы знаний путем выдвижения гипотез и построения их обоснования. Т. е. происходит самообучение на примерах.

·        Происходит анализ имеющихся знаний, при обнаружении противоречий между старыми знаниями и вновь полученными от эксперта или выведенными эмпирически экспертная система  обращается к пользователю, требуя разрешения конфликта.

Продукция

Способ представления процедурных знаний в следующем наиболее общем виде:

(i); Q; Р; С; АèВ; N.

Здесь (i) — собственное имя (метка) продукции;

Q — сфера применения продукции, вычленяющая из предметной области некоторую ее часть, в которой знание, заключенное в продукции, имеет смысл;

P — предусловие, содержащее информацию об истинности данной продукция, ее приоритетности и т.п., используемую в стратегиях управления выводом для выбора данной продукции для исполнения;

С — условие, представляющее собой предикат, истинное значение которого разрешает применять на некотором шаге данную продукцию; АèВ — ядро продукции (интерпретация ядра может быть различной, например: "Если А истинно, то В истинно", "Если А имеется в базе знаний, то В надо внести в базу знаний", "Если А — текущая ситуация, то надо делать B" и т.п.);

N - постусловие продукции, содержащее информацию о том, какие изменения надо внести в данную продукцию или другие продукции, входящие в систему продукций, после выполнения данной продукции.

Примером реализации продукций является язык Пролог.

Психологическая теория интеллекта

Вся мировая история, основанная на блестящих догадках, изобретениях и открытиях, свидетельствует о том, что человек, безусловно, разумен. Психологической основой разумности является интеллект. В общем виде интеллект - это система психических механизмов, которая обуславливает возможность построения "внутри" индивидуума субъективной картины происходящего.

Классические исследования интеллекта человека с помощью тестов показали невозможность оценить интеллект с помощью какого-либо одного параметра (например, способность решать задачи) или нескольких параметров. Ибо, пытаясь построить строить теории интеллекта и тем более теории структуры интеллекта, тестологи описывали своего рода психологическую квазиреальность, вызванную к жизни их собственными изощренными усилиями. Следствием явилась иллюзия "исчезновения" интеллекта как реального психологического процесса. Трудности идентификации результатов интеллектуального тестирования вынудили сторонников тестологического подхода перейти либо на операциональное определение интеллекта (интеллект - это то, что измеряют тесты интеллекта) либо на определения с помощью подбора "примеров" интеллектуального поведения (интеллект - это склонность субъекта вести себя определенным образом в определенной ситуации).

Мы примем следующее определение (Марина Холодная):

Интеллект – форма ментального (умственного) опыта.

Такое определение показывает, что объяснить природу интеллекта на уровне анализа его проявлений невозможно.

Еще одно следствие:

"В пустую голову никакая информация вообще попасть не может. А если бы даже она туда и попала, то ее упорядочивание и преобразование было бы невозможно".

 

Три слоя ментального опыта:

1.     Когнитивный опыт (cognitio - лат. - знание, познание) - хранение, упорядочивание и трансформация наличной и поступающей информации.

2.     Метакогнитивный опыт  - сознательная и непроизвольная организация собственной интеллектуальной активности.

3.     Интенциональный опыт  (intentio – лат. – стремление; направленность сознания, мышления на какой-либо предмет, намерение, цель) - субъективные критерии выбора (в предметной области) источников информации, направления поиска решения.

 

Чтобы оценить индивидуальный склад ума,  надо ответить на вопросы:

ð     Как человек перерабатывает поступающую информацию?

ð     Может ли он контролировать работу своего интеллекта?

ð     Почему именно так и именно об этом он думает?

ð     Как он использует свой интеллект?

Разделы с точки зрения конечного результата

Программно-прагматическое направление

·     Интеллектуальные программы (программы решения интеллектуальных задач).

·     Работа со знаниями (теория и программы)

·     Интеллектуальное программирование (теория и сервисные интеллектуальные программы)

·     Интеллектуальные программные системы

Интеллектуальные программы

Игровые программы

                Человеческие игры

                          Переборные игры

                          Топологические игры

                          Стохастические игры

                Компьютерные игры

                          Игры с жесткой схемой

                          Игры со сценарием

Естественно-языковые программы

                Машинный перевод

                Автоматическое реферирование

                Генерация (синтез) текстов

                         Прозаические тексты

                         Поэтические тексты

Музыкальные программы

                Сочинение музыкальных произведений

                Анализ музыкальных произведений

                Имитация исполнительского стиля

Распознающие и узнающие программы

Программы создания произведений графики и живописи

Прочие программы

                Модели поведения

                Программы доказательства теорем

                Эвристические программы

Семантическая сеть

Сеть (network) - это пятерка H=<A,B,P,P1,C>,

где A - множество вершин;

B - множество имен (весов) вершин;

P - множество дуг, соединяющих пары вершин;

P1 - множество отмеченных входных и выходных дуг;

C - множество весов (имен) дуг.

Семантическая сеть - это сеть, в вершинах которой информационные единицы, а дуги характеризуют отношения и связи между ними.

Для примера на рисунках приведены две семантические сети. Первая сеть (рис. 1.1) соответствует тексту: "В центре комнаты стоит стол. Слева от него окно. У стола глубокое удобное кресло. Недалеко от него столик с телефоном".

Комната                                                                           Окно

           быть в центре            быть слева

                                   

                                              Стол

                   

                  находиться у

Глубокое, удобное кресло

 

  быть недалеко        

                    Столик

                              быть на

                                

                                Телефон

Рис. 1.1. Мебель в комнате

Кафе открыто                                                  Отказ от покупки

                                                нет

           да

Зайти в кафе                                      нет                                  нет

 

Есть мороженое?                                               Есть ли деньги?

                                               есть

                                                                                                есть

                                                                             Купить мороженое

Рис. 1.2. Покупка мороженого в кафе

Вторая сеть (рис. 1.2) описывает набор процедур, необходимых для покупки мороженого в кафе. Если в вершинах первой сети находятся некоторые объекты (стол, комната и т.д.), то в вершинах второй сети названы процедуры. Дуги во второй сети не именованы, так как все они тут имеют одинаковый смысл: "перейти к процедуре".

Семантическая сеть является наиболее общей моделью представления знаний, но она осталась скорее теоретической моделью. Семантическую сеть можно реализовать без ограничений с помощью языка искусственного интеллекта Лисп.

Требования к современным экспертным системам

Если экспертные системы первого поколения рассматривались как машины для логического вывода, то экспертные системы второго поколения рассматриваются как усилители интеллектуальных возможностей человека.

Перечислим требования к современным экспертным системам.

 

у кого сформированы механизмы приобретения,

Умен не тот,  кто знает, а тот, у кого сформированы механизмы приобретения, организации и применения знаний.
Конфуций:
"Обладаю ли я знаниями? Нет. Но когда низкий человек спросит меня о чем-либо, то, даже если я не буду ничего знать, смогу рассмотреть этот вопрос с двух сторон и обо всем рассказать ему".

Вывод знаний

Совокупность программных средств, обеспечивающих поиск, хранение, преобразование и запись в памяти компьютера сложно структурированных информационных единиц (знаний) называется базой знаний. В отличие от базы данных база знаний может содержать теоремы - частные случай продукционных правил с вполне определенными свойствами. Вывод знаний - получение новых информационных единиц из ранее известных.

Перечислим основные формы вывода знаний.

· Вывод абдуктивный

Вывод на основании абдукции - правдоподобного заключения от частного к частному.

·        Вывод вероятностный

Вывод, при котором каждое выражение, используемое в нем, имеет оценку правдоподобия в виде вероятности того, что оно является истинным. При таком выводе применяются специальные процедуры для вычисления вероятности истинного значения результирующего выражения по вероятностям посылок, используемых при выводе.

·        Вывод естественный

Вывод, полученный на основании "здравого смысла". Эта форма вывода может либо соответствовать логическому выводу в некоторой формальной системе (но быть для человека очевидным), либо опираться на соображения, которые не укладываются в строгие рамки формальной системы.

·        Вывод индуктивный

Вывод "от частного к общему". Позволяет на основании обобщения частных примеров некоторого явления выдвинуть гипотезу о существовании общей закономерности. В интеллектуальных системах, использующих индуктивный вывод, работают механизмы, позволяющие при формировании гипотезы приписывать ей оценку правдоподобия (например, вероятность того, что данная гипотеза является истинной). Индуктивный вывод является средством получения новых знаний в интеллектуальных системах.

·        Вывод интуиционистский

Вывод, характерный для интуиционистской логики, не использующий, в частности, закон снятия двойного отрицания и закон исключенного третьего.

·        Вывод логический
Последовательность рассуждений, приводящая от посылок к следствию с использованием аксиом и правил вывода. Такой вывод осуществляется в формальных аксиоматических системах, например, в логике предикатов первого порядка.
·        Вывод на знаниях
Вывод, использующий в качестве посылок выражения, хранящиеся в базе знаний. Вывод на знаниях может быть достоверным, если эти выражения являются достоверными, или правдоподобным, если они снабжены оценками правдоподобия. Как правило, процедуры вывода включают поиск необходимых фрагментов знаний для вывода, т.е. процедуру поиска по образцу.
·        Вывод обратный
Вывод, при котором поиск доказательства начинается с целевого утверждения. Выясняются условия, при которых целевое утверждение является выводимым. Эти условия принимаются за новые целевые утверждения, и процесс поиска продолжается. Вывод заканчивается, когда все очередные условия оказываются аксиомами или процесс обрывается, не приведя к аксиомам. Обратный вывод реализован в алгоритме интерпретатора языка Пролог.
·        Вывод по аналогии
Вывод, основанный на перенесении рассуждения из одной области на другую область, похожую на исследованную. Если имеется вывод А Þ В и область, в которой определено А, гомоморфна области, где определена С, а область, где определено В, гомоморфна области, где определено D, то вывод А Þ B  порождает вывод С Þ В. Вывод по аналогии есть частный случай правдоподобного вывода.
·        Вывод правдоподобный
Вывод, при котором каждый его шаг сопровождается вычислением оценки достоверности полученного утверждения. Частными случаями правдоподобного вывода являются, например, вывод вероятностный и вывод индуктивный.
·        Вывод прямой
Вывод, ведущий от исходных аксиом к целевому выражению.При прямом выводе из-за неоднозначности выбора применяемых аксиом и правил вывода образуется дерево решений и процесс нахождения цепочки, ведущей от исходных аксиом к целевому выражению, является переборным. Стандартной процедурой, используемой при обходе дерева решений, является процедура возврата — бектрекинг.

Задача о кубиках. Общий метод решения задач

Задача состоит в выработке плана переупорядочивания кубиков, поставленных друг на друга, как показано на рис. 2.1. На каждом шагу разрешается переставлять только один кубик. Кубик можно взять только тогда, когда его верхняя поверхность свободна. Кубик можно поставить на стол, либо на другой кубик. Для того чтобы построить требуемый план, мы должны отыскать последовательность ходов, реализующую заданную трансформацию.

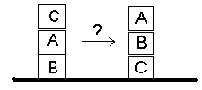Рис. 2.1. Задача перестановки кубиков

Эту задачу можно представлять себе как задачу выбора среди множества возможных альтернатив. В исходной ситуации альтернатива всего одна: поставить кубик C на стол. После того, как кубик C поставлен на стол, мы имеем три альтернативы:

·        поставить A на стол или

·        поставить A на C, или

·        поставить C на A.

Ясно, что альтернативу "поставить C на стол" не имело смысла рассматривать всерьез, так как этот ход никак не влияет на ситуацию.

Как показывает рассмотренный пример, с задачами такого рода связано два типа понятий:

·        проблемные ситуации;

·        разрешенные ходы или действия, преобразующие одни проблемные ситуации в другие.

Проблемные ситуации вместе с возможными ходами образуют направленный (ориентированный) граф, называемый пространством состояний. Пространство состояний для только что рассмотренного примера дано на  рис. 2.2. Вершины графа соответствуют проблемным ситуациям, дуги - разрешенным переходам из одних состояний в другие. Проблема отыскания плана решения задачи эквивалентна проблеме построения пути между заданной начальной ситуацией ("стартовой" вершиной) и некоторой указанной заранее конечной ситуацией, называемой также целевой вершиной.

                                             

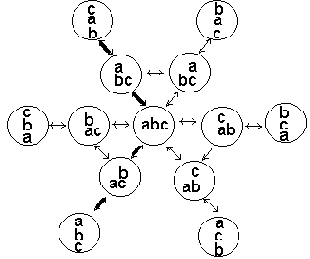Рис. 2.2. Графическое представление задачи манипулирования

                   кубиками. Выделенный путь является решением задачи
Нетрудно построить аналогичное представление в виде графа и для других популярных головоломок. Наиболее очевидные примеры - это задача о "ханойской башне" и задача о перевозке через реку волка, козы и капусты.
Пространство состояний некоторой задачи определяет "правила игры": вершины пространства состояний соответствуют ситуациям, а дуги - разрешенным ходам или действиям, или шагам решения задачи. Конкретная задача определяется
·        пространством состояний,
·        стартовой вершиной,
·        целевым условием (т. е. условием, к достижению которого следует стремиться); "целевые вершины" - это вершины, удовлетворяющие этим условиям.
Каждому разрешенному ходу или действию можно приписать его стоимость. Например, в задаче манипуляции кубиками стоимости, приписанные тем или иным перемещениям кубиков, будут указывать нам на то, что некоторые кубики перемещать труднее, чем другие. В задаче о коммивояжере ходы соответствуют переездам из города в город. Ясно, что в данном случае стоимость хода - это расстояние между двумя городами.
В тех случаях, когда каждый ход имеет стоимость, мы заинтересованы в отыскании решения минимальной стоимости. Стоимость решения - это сумма стоимостей дуг, из которых состоит "решающий путь" - путь из стартовой вершины в целевую. Даже если стоимости не заданы, все равно может возникнуть оптимизационная задача: нас может интересовать кратчайшее решение.
Прежде чем будут рассмотрены некоторые программы, реализующие классический алгоритм поиска в пространстве состояний, давайте сначала обсудим, как пространство состояний может быть представлено в прологовской программе.
Мы будем представлять пространство состояний при помощи отношения next(X,Y), которое истинно тогда, когда в пространстве состояний существует разрешенный ход из вершины X в вершину Y.


Мы будем говорить, что Y - это преемник вершины X. Если с ходами связаны их стоимости, мы добавим третий аргумент, стоимость хода: next(X,Y,C). Эти отношения можно задавать в программе явным образом при помощи выбора соответствующих фактов. Однако такой принцип оказывается непрактичным и нереальным для тех типичных случаев, когда пространство состояний устроено достаточно сложно. Поэтому отношение следование next обычно определяется неявно, при помощи правил вычисления вершин-преемников некоторой заданной вершины. Другим вопросом, представляющим интерес с самой общей точки зрения, является вопрос о способе представления состояний, т.е. самих вершин. Это представление должно быть компактным, но в то же время оно должно обеспечивать эффективное выполнение необходимых операций, в частности операций вычисления вершин-преемников, а возможно и стоимостей соответствующих ходов.
Рассмотрим в качестве примера задачу манипулирования кубиками. Мы будем рассматривать общий случай, когда имеется произвольное число кубиков, из которых составлены столбики, - один или несколько. Число столбиков мы ограничим некоторым максимальным числом, скажем 3, чтобы задача была интереснее. Такое ограничение, кроме того, является вполне реальным, поскольку рабочее пространство, которым располагает робот, манипулирующий кубиками, ограничено.
Проблемную ситуацию можно представить как список столбиков. Каждый столбик, в свою очередь, представляется списком кубиков, из которых он составлен. Кубики упорядочены в списке таким образом, что самый верхний список находится в голове списка. "Пустые" столбики изображаются как пустые списки. Таким образом, исходную ситуацию можно записать как терм [[c,a,b], [], []]. Целевая ситуация - это любая конфигурация кубиков, содержащая столбик, составленный из всех имеющихся кубиков в указанном порядке. Таких ситуаций три:
[[a,b,c], [], []]
[[], [a,b,c], []]
[[], [], [a,b,c]]
Отношение следование можно запрограммировать, исходя из следующего правила: ситуация S2 есть преемник ситуации S, если в S имеется два столбика  C1 и C2, такие, что верхний кубик из C1 можно поставить сверху на C2 и получить тем самым S2.Поскольку все ситуации - это списки столбиков, правило транслируется на Пролог так:
next(S, [C1,[Cub|C2]|T]):-            % переставить Cub на столбик C2
        select(S,[Cub|C1],S1),          %  найти первый столбик C1
        select(S1,C2,T).                     % найти второй столбик C2
В нашем примере целевое условие имеет вид:
goal(S):- member([a,b,c],S).

---

---