Алгоритм с ковариациями и с квадратичными описаниями.

Рис.  10. МГУА как эквивалент массовой селекции.

В этом алгоритме [5, 6] используются частные описания, представленные в следующих формулах:

yi=a0+a1xi+a2xj+a3xixj;

yk=a0+a1xi+a2xj+a3xixj+a4xi2+a5xj2.

Сложность модели увеличивается от ряда к ряду селекции как по числу учитываемых аргументов, так и по степени. Степень полного описания быстро растет. На первом ряду — квадратичные описания, на втором — четвертой степени, на третьем — восьмой и т. д. В связи с этим минимум критерия селекции находится быстро, но не совсем точно. Кроме того, имеется опасность потери существенного аргумента, особенно на первых рядах селекции (в случае отсутствия протекции). Специальные теоремы теории МГУА определяют условия, при которых результат селекции не отличается от результата полного перебора моделей.

Для того чтобы степень полного уравнения повышалась с каждым рядом селекции на единицу, достаточно рассматривать все аргументы и их ковариации как обобщенные аргументы и пользоваться составленными для них линейными описаниями.

Алгоритмические модели

Алгоритмические модели основаны на понятии алгоритма. Исторически первые точные определения алгоритма, возникшие в 30-х годах, были связаны с понятием вычислимости. С тех пор было предложено множество, как выяснилось, эквивалентных определений алгоритма.

В практике программирования алгоритмы принято описывать с помощью алгоритмических языков программирования. Широко используются также разного рода блок-схемы алгоритмов, позволяющие представить алгоритмы в наглядном и общедоступном виде, не привлекая в тоже время сложных конструкций из конкретных языков программирования.

Чтобы оценить возможности использования алгоритмов для представления неформальных процедур, рассмотрим простую задачу.

ЗАДАЧА. Описать процедуру, реализующую преобразование из именительного падежа в родительный для существительных следующих типов: ДОМ, МАМА, ВИЛКА, КИНО, НОЧЬ, ТОКАРЬ, КИЛЬ.

Решение 1 указано на Рис.  13 в виде блок схемы соответствующего алгоритма.

Рис.  13. Решение 1. Алгоритм

С точки зрения программирования на алгоритмических языках достоинства подобного представления очевидны — эта блок-схема без затруднений переводится в текст программы, например, на языке Ассемблера или С++. Однако само составление подобной блок-схемы при появлении существительных новых типов становится, очевидно, все более и более утомительным занятием. Для иллюстрации этого предположим, что дана

ДОПОЛНИТЕЛЬНАЯ ЗАДАЧА. Расширить алгоритм, представленный на Рис.  13 на слова ВАСЯ, ВРЕМЯ, АКЦИЯ, ЗАДАЧА.

Разумеется программист без особого труда составит соответствующую блок-схему алгоритма. И все же, если учесть, что подобные изменения и расширения алгоритма при программировании неформальных процедур происходят многократно (реальная сложность неформальной процедуры как раз и проявляется в практической невозможности предусмотреть заранее все случаи), следует признать, что, вполне правильное в статике, решение 1 в динамике неудачно!

Арифметические операторы

Атомы +, -, *, /, mod и div - обычные атомы Пролога и могут использоваться почти в любом контексте. Указанные атомы - не встроенные предикаты, а функторы, имеющие силу только в преде­лах арифметических выражений. Они определены как инфиксные операторы. Эти атомы являются главными функторами в структуре, а сама структура может принимать только описанные выше формы.

Позиция, приоритет и ассоциативность арифметических опера­торов четко заданы и перечислены в таблице операторов в гл. 6.

Арифметический оператор выполняется следующим образом. Во-первых, вычисляются арифметические выражения по обе стороны оператора. Во-вторых, над результатом вычислений выполняется нужная операция.

Арифметические операторы определяются Пролог-системой. Ес­ли мы напишем предикат

среднее (X,Y,Z) :- Z is (X+Y)/2.

то хотя можно определить среднее как оператор

?- ор(250^х, среднее).

но Пролог выдаст сообщение об ошибке, если встретит выражение Z is X среднее Y.

Это произойдет потому, что Х среднее Y не образует арифметиче­ского выражения, а среднее не является арифметическим операто­ром, определенным в системе.

Арифметические выражения

В этой главе показано, каким образом Пролог выполняет ариф­метические операции. Будут описаны арифметические операторы и их использование в выражениях, а также рассмотрены встроенные предикаты, служащие для вычисления и сравнения арифметических выражений.

Арифметическое выражение является числом или структурой. В структуру может входить одна или более компонент, таких, как чис­ла, арифметические операторы, арифметические списковые выраже­ния, переменная, конкретизированная арифметическим выражени­ем, унарные функторы, функторы преобразования и арифметиче­ские функторы.

Числа. Числа и их диапазоны определяются в конкретной реали­зации Пролога.

Арифметические операторы. + - * / mod div

Арифметические списковые выражения. Если Х - арифметиче­ское выражение, то список [X ] также является арифметическим вы­ражением, например [1,2,3]. Первый элемент списка используется как операнд в выражении. Скажем,

X is ([l,2,3]+5)

имеет значение 6.

Арифметические списковые выражения полезны и при обработке символов, поскольку последние могут рассматриваться как неболь­шие целые числа. Например, символ "а" эквивалентен [97 ] и, буду­чи использован в выражении, вычисляется как 97. Поэтому значение выражения «р»+"А"-"а" равно 80, что соответствует коду ASCII для «Р».

Переменная, конкретизированная арифметическим выражени­ем. Примеры:

Х-5+2 и У-3*(2+А)

Унарные функторы. Примеры:

+(Х) и -(У)

Функторы преобразования. В некоторых реализациях Пролога имеется арифметика с плавающей точкой, а следовательно, и функ­торы преобразования. Например:

float (X) преобразует целое число Х в число с плавающей точкой.

Математические функторы. Пример: квадрат(Х) объявлен как оператор и эквивалентен арифметическому выражению (Х*Х).

ATOM

Атом представляет собой произвольную последовательность сим­волов, заключенную в одинарные кавычки. Одинарный символ ка­вычки, встречающийся внутри атома, записывается дважды. Когда атом выводится на печать, внешние символы кавычек обычно не пе­чатаются. Существует несколько исключений, когда атомы необяза­тельно записывать в кавычках. Вот эти исключения:

1) атом, состоящий только из чисел, букв и символа подчеркива­ния и начинающийся со строчной буквы;

2) атом, состоящий целиком из специальных символов. К специ­альным символам относятся:

+ - * / ^ = : ; ? @ $ &

Заметим, что атом, начинающийся с /*, будет воспринят как на­чало комментария, если он не заключен в одинарные кавычки.

Как правило, в программах на Прологе используются атомы без кавычек.

Атом, который необязательно заключать в кавычки, может быть записан и в кавычках. Запись с внешними кавычками и без них опре­деляет один и тот же атом.

Внимание: допустимы случаи, когда атом не содержит ни одного символа (так называемый 'нулевой атом') или содержит непечатае­мые символы. (В Прологе имеются предикаты для построения ато­мов, содержащих непечатаемые или управляющие символы.) При выводе таких атомов на печать могут возникнуть ошибки.

Базовые понятия ИИ

Терминология. Философские аспекты проблемы систем ИИ (возможность существования, безопасность, полезность). История развития систем ИИ.

Лекционные занятия - 4 ч.

Цель преподавания дисциплины

В современном мире прогресс производительности программиста практически достигается только в тех случаях, когда часть интеллектуальной нагрузки берут на себя компьютеры. Одним из способов достигнуть максимального прогресса в этой области, является "искусственный интеллект", когда компьютер берет на себя не только однотипные, многократно повторяющиеся операции, но и сам сможет обучаться. Кроме того, создание полноценного "искусственного интеллекта" открывает перед человечеством новые горизонты развития.

Целью изучения дисциплины является подготовка специалистов в области автоматизации сложноформализуемых задач, которые до сих пор считаются прерогативой человека. Задачей изучения дисциплины является приобретение знаний о способах мышления человека, а так же о методах их реализации на компьютере.

Основным предметом изучения дисциплины являются мыслительные способности человека и способы их реализации техническими средствами.

ЧИСЛА

Большинство реализации Пролога поддерживают целые и дейст­вительные числа. Для того чтобы выяснить, каковы диапазоны и точ­ность, чисел следует обратиться к руководству по конкретной реали­зации.

Философские аспекты проблемы систем ИИ (возможность существования, безопасность, полезность).

С курсом "Основы проектирования систем ИИ" сложилась ситуация, которая роднит его с коммунизмом — изучается то, чего еще нет. И если этого не будет в течение ближайших 100 лет, то очень может быть, что эпоха ИИ на этом окончится.

Исходя из сказанного выше, вытекает основная философская проблема в области ИИ — возможность или не возможность моделирования мышления человека. В случае если когда-либо будет получен отрицательный ответ на этот вопрос, то все остальные вопросы курса не будут иметь не малейшего смысла.

Следовательно, начиная исследование ИИ, мы заранее предполагаем положительный ответ. Попробуем привести несколько соображений, которые подводят нас к данному ответу.

  Первое доказательство является схоластическим, и доказывает непротиворечивость ИИ и Библии. По-видимому, даже люди далекие от религии, знают слова священного писания: "И создал Господь человека по образу и подобию своему …". Исходя из этих слов, мы можем заключить, что, поскольку Господь, во-первых, создал нас, а во-вторых, мы по своей сути подобны ему, то мы вполне можем создать кого-то по образу и подобию человека.

  Создание нового разума биологическим путем для человека дело вполне привычное. Наблюдая за детьми, мы видим, что большую часть знаний они приобретают путем обучения, а не как заложенную в них заранее. Данное утверждение на современном уровне не доказано, но по внешним признакам все выглядит именно так.

  То, что раньше казалось вершиной человеческого творчества — игра в шахматы, шашки, распознавание зрительных и звуковых образов, синтез новых технических решений, на практике оказалось не таким уж сложным делом (теперь работа ведется не на уровне возможности или невозможности реализации перечисленного, а о нахождении наиболее оптимального алгоритма). Теперь зачастую данные проблемы даже не относят к проблемам ИИ. Есть надежда, что и полное моделирование мышления человека окажется не таким уж и сложным делом.

  С проблемой воспроизведения своего мышления тесно смыкается проблема возможности самовоспроизведения.

Способность к самовоспроизведению долгое время считалась прерогативой живых организмов. Однако некоторые явления, происходящие в неживой природе (например, рост кристаллов, синтез сложных молекул копированием), очень похожи на самовоспроизведение. В начале 50-х годов Дж. фон Нейман занялся основательным изучением самовоспроизведения и заложил основы математической теории "самовоспроизводящихся автоматов". Так же он доказал теоретически возможность их создания.

Существуют также различные неформальные доказательства возможности самовоспроизведения, но для программистов самым ярким доказательством, пожалуй, будет существование компьютерных вирусов.

  Принципиальная возможность автоматизации решения интеллектуальных задач с помощью ЭВМ обеспечивается свойством алгоритмической универсальности. Что же это за свойство?

Алгоритмическая универсальность ЭВМ означает, что на них можно программно реализовывать (т. е. представить в виде машинной программы) любые алгоритмы преобразования информации, — будь то вычислительные алгоритмы, алгоритмы управления, поиска доказательства теорем или композиции мелодий. При этом мы имеем в виду, что процессы, порождаемые этими алгоритмами, являются потенциально осуществимыми, т. е. что они осуществимы в результате конечного числа элементарных операций. Практическая осуществимость алгоритмов зависит от имеющихся в нашем распоряжении средств, которые могут меняться с развитием техники. Так, в связи с появлением быстродействующих ЭВМ стали практически осуществимыми и такие алгоритмы, которые ранее были только потенциально осуществимыми.

Однако свойство алгоритмической универсальности не ограничивается констатацией того, что для всех известных алгоритмов оказывается возможной их программная реализация на ЭВМ. Содержание этого свойства имеет и характер прогноза на будущее: всякий раз, когда в будущем какое-либо предписание будет признано алгоритмом, то независимо от того, в какой форме и какими средствами это предписание будет первоначально выражено, его можно будет задать также в виде машинной программы.



Однако не следует думать, что вычислительные машины и роботы могут в принципе решать любые задачи. Анализ разнообразных задач привел математиков к замечательному открытию. Было строго доказано существование таких типов задач, для которых невозможен единый эффективный алгоритм, решающий все задачи данного типа; в этом смысле невозможно решение задач такого типа и с помощью вычислительных машин. Этот факт способствует лучшему пониманию того, что могут делать машины и чего они не могут сделать. В самом деле, утверждение об алгоритмической неразрешимости некоторого класса задач является не просто признанием того, что такой алгоритм нам не известен и никем еще не найден. Такое утверждение представляет собой одновременно и прогноз на все будущие времена о том, что подобного рода алгоритм нам не известен и никем не будет указан или, и иными словами, что он не существует.

Как же действует человек при решении таких задач? Похоже, что он просто-напросто игнорирует их, что, однако не мешает ему жить дальше. Другим путем является сужение условий универсальности задачи, когда она решается только для определенного подмножества начальных условий. И еще один путь заключается в том, что человек методом "научного тыка" расширяет множество доступных для себя элементарных операций (например, создает новые материалы, открывает новые месторождения или типы ядерных реакций).

Следующим философским вопросом ИИ является цель создания. В принципе все, что мы делаем в практической жизни, обычно направлено на то, чтобы больше ничего не делать. Однако при достаточно высоком уровне жизни (большом количестве потенциальной энергии) человека на первые роли выступает уже не лень (в смысле желания экономить энергию), а поисковые инстинкты. Допустим, что человек сумел создать интеллект, превышающий свой собственный (пусть не качеством, так количеством). Что теперь будет с человечеством? Какую роль будет играть человек? Для чего он теперь нужен? Не станет ли он тупой и жирной свиньей? И вообще, нужно ли в принципе создание ИИ?



По-видимому, самым приемлемым ответом на эти вопросы является концепция "усилителя интеллекта" (УИ). Я думаю, что здесь уместна аналогия с президентом государства — он не обязан знать валентности ванадия или языка программирования Java для принятия решения о развитии ванадиевой промышленности. Каждый занимается своим делом — химик описывает технологический процесс, программист пишет программу; в конце концов, экономист говорит президенту, что вложив деньги в промышленный шпионаж, страна получит 20%, а в ванадиевую промышленность — 30% годовых. Думаю, что при такой постановке вопроса даже самый последний бомж (правда находящийся в сознании) сможет сделать правильный выбор.

В данном примере президент использует биологический УИ — группу специалистов с их белковыми мозгами. Но уже сейчас используются и неживые УИ — например мы не могли бы предсказать погоду без компьютеров, при полетах космических кораблей с самого начала использовались бортовые счетно-решающие устройства. Кроме того, человек уже давно использует усилители силы (УС) — понятие, во многом аналогичное УИ. В качестве усилителей силы ему служат автомобили, краны, электродвигатели, прессы, пушки, самолеты и многое-многое другое.

Основным отличием УИ от УС является наличие воли. Ведь мы не сможем себе представить, чтобы вдруг серийный "Запорожец" взбунтовался, и стал ездить так, как ему хочется. Не можем представить именно потому, что ему ничего не хочется, у него нет желаний. В тоже время, интеллектуальная система, вполне могла бы иметь свои желания, и поступать не так, как нам хотелось бы. Таким образом перед нами встает еще одна проблема — проблема безопасности.

Данная проблема будоражит умы человечества еще со времен Карела Чапека, впервые употребившего термин "робот". Большую лепту в обсуждение данной проблемы внесли и другие писатели-фантасты. Как самые известные мы можем упомянуть серии рассказов писателя-фантаста и ученого Айзека Азимова, а так же довольно свежее произведение — "Терминатор".


Кстати именно у Айзека Азимова мы можем найти самое проработанное, и принятое большинством людей решение проблемы безопасности. Речь идет о так называемых трех законах роботехники.

  Робот не может причинить вред человеку или своим бездействием допустить, чтобы человеку был причинен вред.

  Робот должен повиноваться командам, которые ему дает человек, кроме тех случаев, когда эти команды противоречат первому закону.

  Робот должен заботиться о своей безопасности, насколько это не противоречит первому и второму закону.

На первый взгляд подобные законы, при их полном соблюдении, должны обеспечить безопасность человечества. Однако при внимательном рассмотрении возникают некоторые вопросы. Во-первых, законы сформулированы на человеческом языке, который не допускает простого их перевода в алгоритмическую форму. Попробуйте, к примеру перевести на любой из известных Вам языков программирования, такой термин, как "причинить вред". Или "допустить". Попробуйте определить, что происходит в любом случае, а что он "допустил"?

Далее предположим, что мы сумели переформулировать, данные законы на язык, который понимает автоматизированная система. Теперь интересно, что будет подразумевать система ИИ под термином "вред" после долгих логических размышлений? Не решит ли она, что все существования человека это сплошной вред? Ведь он курит, пьет, с годами стареет и теряет здоровье, страдает. Не будет ли меньшим злом быстро прекратить эту цепь страданий? Конечно можно ввести некоторые дополнения, связанные с ценностью жизни, свободой волеизъявления. Но это уже будут не те простые три закона, которые были в исходнике.

Следующим вопросом будет такой. Что решит система ИИ в ситуации, когда спасение одной жизни возможно только за счет другой? Особенно интересны те случаи, когда система не имеет полной информации о том, кто есть кто.

Однако несмотря на перечисленные проблемы, данные законы являются довольно неплохим неформальным базисом проверки надежности системы безопасности для систем ИИ.



Так что же, неужели нет надежной системы безопасности? Если отталкиваться от концепции УИ, то можно предложить следующий вариант.

Согласно многочисленным опытам, несмотря на то, что мы не знаем точно, за что отвечает каждый отдельный нейрон в человеческом мозге, многим из наших эмоций обычно соответствует возбуждение группы нейронов (нейронный ансамбль) во вполне предсказуемой области. Были также проведены обратные эксперименты, когда раздражение определенной области вызывало желаемый результат. Это могли быть эмоции радости, угнетения, страха, агрессивности. Это наводит на мысль, что в принципе мы вполне могли бы вывести степень "довольности" организма наружу. В то же время, практически все известные механизмы адаптации и самонастройки (в первую очередь имеются в виду технические системы), базируются на принципах типа "хорошо" — "плохо". В математической интерпретации это сведение какой-либо функции к максимуму или к минимуму. Теперь представим себе, что наш УИ в качестве такой функции использует измеренную прямо или косвенно, степень удовольствия мозга человека-хозяина. Если принять меры, чтобы исключить самодеструктивную деятельность в состоянии депрессии, а так же предусмотреть другие особые состояния психики, то получим следующее.

Поскольку предполагается, что нормальный человек, не будет наносить вред самому себе, и, без особой на то причины, другим, а УИ теперь является частью данного индивидуума (не обязательно физическая общность), то автоматически выполняются все 3 закона роботехники. При этом вопросы безопасности смещаются в область психологии и правоохранения, поскольку система (обученная) не будет делать ничего такого, чего бы не хотел ее владелец.

И теперь осталась еще одна тема — а стоит ли вообще создавать ИИ, может просто закрыть все работы в этой области? Единственное, что можно сказать по этому поводу — если ИИ возможно создать, то рано или поздно он будет создан. И лучше его создавать под контролем общественности, с тщательной проработкой вопросов безопасности, чем он будет создан лет через 100-150 (если к тому времени человечество еще не уничтожит само себя) каким-нибудь программистом-механиком-самоучкой, использующим достижения современной ему техники.Ведь сегодня, например, любой грамотный инженер, при наличии определенных денежных ресурсов и материалов, может изготовить атомную бомбу.

Геометрический и структурный подходы.

Каждый раз, когда сталкиваются с незнакомыми задачами, появляется естественное желание представить их в виде некоторой легко понимаемой модели, которая позволяла бы осмыслить задачу в таких терминах, которые легко воспроизводятся нашим воображением. А так как мы существуем в пространстве и во времени, наиболее понятной для нас является пространственно-временная интерпретация задач.

Любое изображение, которое возникает в результате наблюдения какого-либо объекта в процессе обучения или экзамена, можно представить в виде вектора, а значит и в виде точки некоторого пространства признаков. Если утверждается, что при показе изображений возможно однозначно отнести их к одному из двух (или нескольких) образов, то тем самым утверждается, что в некотором пространстве существует две (или несколько) области, не имеющие общих точек, и что изображения — точки из этих областей. Каждой такой области можно приписать наименование, т. е. дать название, соответствующее образу.

Проинтерпретируем теперь в терминах геометрической картины процесс обучения распознаванию образов, ограничившись пока случаем распознавания только двух образов. Заранее считается известным лишь только то, что требуется разделить две области в некотором пространстве и что показываются точки только из этих областей. Сами эти области заранее не определены, т. е. нет каких-либо сведений о расположении их границ или правил определения принадлежности точки к той или иной области.

В ходе обучения предъявляются точки, случайно выбранные из этих областей, и сообщается информация о том, к какой области принадлежат предъявляемые точки. Никакой дополнительной информации об этих областях, т. е. о расположении их границ, в ходе обучения не сообщается. Цель обучения состоит либо в построении поверхности, которая разделяла бы не только показанные в процессе обучения точки, но и все остальные точки, принадлежащие этим областям, либо в построении поверхностей, ограничивающих эти области так, чтобы в каждой из них находились только точки одного образа.
Иначе говоря, цель обучения состоит в построении таких функций от векторов-изображений, которые была бы, например, положительны на всех точках одного и отрицательны на всех точках другого образа. В связи с тем, что области не имеют общих точек, всегда существует целое множество таких разделяющих функций, а в результате обучения должна быть построена одна из них.

Если предъявляемые изображения принадлежат не двум, а большему числу образов, то задача состоит в построении по показанным в ходе обучения точкам поверхности, разделяющей все области, соответствующие этим образам, друг от друга. Задача эта может быть решена, например, путем построения функции, принимающей над точками каждой из областей одинаковое значение, а над точками из разных областей значение этой функции должно быть различно.

Рис.  2. Два образа.

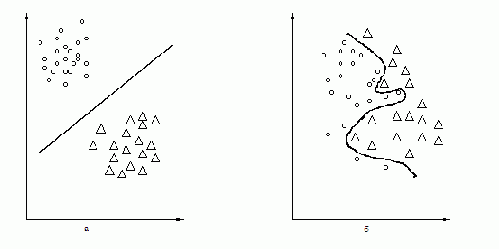
На первый взгляд кажется, что знание всего лишь некоторого количества точек из области недостаточно, чтобы отделить всю область. Действительно, можно указать бесчисленное количество различных областей, которые содержат эти точки, и как бы ни была построена по ним поверхность, выделяющая область, всегда можно указать другую область, которая пересекает поверхность и вместе с тем содержит показанные точки. Однако известно, что задача о приближении функции по информации о ней в ограниченном множестве точек, существенно более узкой, чем все множество, на котором функция задана, является обычной математической задачей об аппроксимации функций. Разумеется, решение таких задач требует введения определенных ограничений на классе рассматриваемых функций, а выбор этих ограничений зависит от характера информации, которую может добавить учитель в процессе обучения. Одной из таких подсказок является гипотеза о компактности образов. Интуитивно ясно, что аппроксимация разделяющей функции будет задачей тем более легкой, чем более компактны и чем более разнесены в пространстве области, подлежащие разделению. Так, например, в случае, показанном на Рис.  2а, разделение заведомо более просто, чем в случае, показанном на Рис.  2б.


Действительно, в случае, изображенном на Рис.  2а, области могут быть разделены плоскостью, и даже при больших погрешностях в определении разделяющей функции она все же будет продолжать разделять области. В случае же на Рис.  2б, разделение осуществляется замысловатой поверхностью и даже незначительные отклонения в ее форме приводят к ошибкам разделения. Именно это интуитивное представление о сравнительно легко разделимых областях привело к гипотезе компактности.

Наряду с геометрической интерпретацией проблемы обучения распознаванию образов существует и иной подход, который назван структурным, или лингвистическим. Поясним лингвистический подход на примере распознавания зрительных изображений. Сначала выделяется набор исходных понятий — типичных фрагментов, встречающихся на изображениях, и характеристик взаимного расположения фрагментов — "слева", "снизу", "внутри" и т. д. Эти исходные понятия образуют словарь, позволяющий строить различные логические высказывания, иногда называемые предположениями. Задача состоит в том, чтобы из большого количества высказываний, которые могли бы быть построены с использованием этих понятий, отобрать наиболее существенные для данного конкретного случая.

Далее, просматривая конечное и по возможности небольшое число объектов из каждого образа, нужно построить описание этих образов. Построенные описания должны быть столь полными, чтобы решить вопрос о том, к какому образу принадлежит данный объект. При реализации лингвистического подхода возникают две задачи: задача построения исходного словаря, т. е. набор типичных фрагментов, и задача построения правил описания из элементов заданного словаря.

В рамках лингвистической интерпретации проводится аналогия между структурой изображений и синтаксисом языка. Стремление к этой аналогии было вызвано возможностью использовать аппарат математической лингвистики, т. е. методы по своей природе являются синтаксическими. Использование аппарата математической лингвистики для описания структуры изображений можно применять только после того, как произведена сегментация изображений на составные части, т.е. выработаны слова для описания типичных фрагментов и методы их поиска. После предварительной работы, обеспечивающей выделение слов, возникают собственно лингвистические задачи, состоящие из задач автоматического грамматического разбора описаний для распознавания изображений. При этом проявляется самостоятельная область исследований, которая требует не только знания основ математической лингвистики, но и овладения приемами, которые разработаны специально для лингвистической обработки изображений.

Гипотеза компактности

Если предположить, что в процессе обучения пространство признаков формируется исходя из задуманной классификации, то тогда можно надеяться, что задание пространство признаков само по себе задает свойство, под действием которого образы в этом пространстве легко разделяются. Именно эти надежды по мере развития работ в области распознавания образов стимулировали появление гипотезы компактности, которая гласит: образам соответствуют компактные множества в пространстве признаков. Под компактным множеством пока будем понимать некие "сгустки" точек в пространстве изображений, предполагая, что между этими сгустками существуют разделяющие их разряжения.

Однако эту гипотезу не всегда удавалось подтвердить экспериментально, но, что самое главное, те задачи, в рамках которых гипотеза компактности хорошо выполнялась (Рис.  2а), все без исключения находили простое решение. И наоборот, те задачи, для которых гипотеза не подтверждалась (Рис.  2б), либо совсем не решались, либо решались с большим трудом с привлечением дополнительных ухищрений. Этот факт заставил по меньшей мере усомниться в справедливости гипотезы компактности, так как для опровержения любой гипотезы достаточно одного отрицающего ее примера. Вместе с этим, выполнение гипотезы всюду там, где удавалось хорошо решить задачу обучения распознаванию образов, сохраняло к этой гипотезе интерес. Сама гипотеза компактности превратилась в признак возможности удовлетворительного решения задач распознавания.

Формулировка гипотезы компактности подводит вплотную к понятию абстрактного образа. Если координаты пространства выбирать случайно, то и изображения в нем будут распределены случайно. Они будут в некоторых частях пространства располагаться более плотно, чем в других. Назовем некоторое случайно выбранное пространство абстрактным изображением. В этом абстрактном пространстве почти наверняка будут существовать компактные множества точек. Поэтому в соответствии с гипотезой компактности множества объектов, которым в абстрактном пространстве соответствуют компактные множества точек, разумно назвать абстрактными образами данного пространства.

Иерархическое группирование

Рис.  12. Результаты работы иерархической агломеративной процедуры группирования объектов, представленные в виде дендрограммы.

Классификационные процедуры иерархического типа предназначены для получения наглядного представления о стратификационной структуре всей исследуемой совокупности объектов. Эти процедуры основаны на последовательном объе­динении кластеров (агломеративные процедуры) и на последо­вательном разбиении (дивизимные процедуры). Наибольшее распространение получили агломеративные процедуры. Рас­смотрим последовательность операций в таких процедурах.

На первом шаге все объекты считаются отдельными кла­стерами. Затем на каждом последующем шаге два ближайших кластера объединяются в один. Каждое объединение уменьшает число кластеров на один так, что в конце концов все объекты объединяются в один кластер. Наиболее подходящее разбиение выбирает чаще всего сам исследователь, которому предостав­ляется дендрограмма, отображающая результаты группирования объектов на всех шагах алгоритма (Рис.  12). Могут од­новременно также использоваться и математические критерии качества группирования.

Различные варианты определения расстояния между кла­стерами дают различные варианты иерархических агломеративных процедур. Учитывая специфику подобных процедур, для задания расстояния между классами оказывается достаточным указать порядок пересчета расстояний между классом wl и классом w(m, n) являющимся объединением двух других классов wm и wn по расстояниям qmn = q(wm, wn) и qln = q(wl, wn) между этими классами. В литературе предлагается следующая общая формула для вычисления расстояния между некоторым классом wl и классом w(m, n):

ql(m, n) = q (wl, w(m, n)) = aqlm + bqln + gqmn + d | qlm  - qln |

где a, b, g и d — числовые коэффициенты, определяющие на­целенность агломеративной процедуры на решение той или иной экстремальной задачи. В частности, полагая a = b = -d = ½ и g = 0, приходим к расстоянию, измеряемому по принципу ближайшего соседа.
Если положить a = b = d = ½ и g = 0, то расстояние между двумя классами определится как расстояние между двумя самыми далекими объектами этих классов, то есть это будет расстояние дальнего соседа. И, наконец, выбор коэффициентов соотношения по формулам

приводит к расстоянию qcp между классами, вычисленному как среднее расстояние между всеми парами объектов, один из ко­торых берется из одного класса, а другой из другого.

Использование следующей модификации формулы



дает агломеративный алгоритм, приводящий к минимальному увеличению общей суммы квадратов расстояний между объек­тами внутри классов на каждом шаге объединения этих классов. В отличие от оптимизационных кластерных алгоритмов предоставляющих исследователю конечный результат группирования объектов, иерархические процедуры позволяют проследить процесс выделения группировок и иллюстрируют соподчиненность кластеров, образующихся на разных шагах ка­кого-либо агломеративного или дивизимного алгоритма. Это стимулирует воображение исследователя и помогает ему привлекать для оценки структуры данных дополнительные формальные и неформальные представления.

История исследований в области нейронных сетей

Возвратимся немного назад, и рассмотрим историю исследований нейронных сетей.

В истории исследований в области нейронных сетей, как и в истории любой другой науки, были свои успехи и неудачи. Кроме того, здесь постоянно сказывается психологический фактор, проявляющийся в неспособности человека описать словами то, как он думает.

Способность нейронной сети к обучению впервые исследована Дж. Маккалоком и У. Питтом. В 1943 году вышла их работа “Логическое исчисление идей, относящихся к нервной деятельности", в которой была построена модель нейрона, и сформулированы принципы построения искусственных нейронных сетей.

Крупный толчок развитию нейрокибернетики дал американский нейрофизиолог Френк Розенблатт, предложивший в 1962 году свою модель нейронной сети — персептрон. Воспринятый первоначально с большим энтузиазмом, он вскоре подвергся интенсивным нападкам со стороны крупных научных авторитетов. И хотя подробный анализ их аргументов показывает, что они оспаривали не совсем тот персептрон, который предлагал Розенблатт, крупные исследования по нейронным сетям были свернуты почти на 10 лет.

Несмотря на это в 70-е годы было предложено много интересных разработок, таких, например, как когнитрон, способный хорошо распознавать достаточно сложные образы независимо от поворота и изменения масштаба изображения.

В 1982 году американский биофизик Дж. Хопфилд предложил оригинальную модель нейронной сети, названную его именем. В последующие несколько лет было найдено множество эффективных алгоритмов: сеть встречного потока, двунаправленная ассоциативная память и др.

В киевском институте кибернетики с 70-х годов ведутся работы над стохастическими нейронными сетями.

История развития систем ИИ.

Исторически сложились три основных направления в моделировании ИИ.

В рамках первого подхода объектом исследований являются структура и механизмы работы мозга человека, а конечная цель заключается в раскрытии тайн мышления. Необходимыми этапами исследований в этом направлении являются построение моделей на основе психофизиологических данных, проведение экспериментов с ними, выдвижение новых гипотез относительно механизмов интеллектуальной деятельности, совершенствование моделей и т. д.

Второй подход в качестве объекта исследования рассматривает ИИ. Здесь речь идет о моделировании интеллектуальной деятельности с помощью вычислительных машин. Целью работ в этом направлении является создание алгоритмического и программного обеспечения вычислительных машин, позволяющего решать интеллектуальные задачи не хуже человека.

Наконец, третий подход ориентирован на создание смешанных человеко-машинных, или, как еще говорят, интерактивных интеллектуальных систем, на симбиоз возможностей естественного и искусственного интеллекта. Важнейшими проблемами в этих исследованиях является оптимальное распределение функций между естественным и искусственным интеллектом и организация диалога между человеком и машиной.

Самыми первыми интеллектуальными задачами, которые стали решаться при помощи ЭВМ были логические игры (шашки, шахматы), доказательство теорем. Хотя, правда здесь надо отметить еще кибернетические игрушки типа "электронной мыши" Клода Шеннона, которая управлялась сложной релейной схемой. Эта мышка могла "исследовать" лабиринт, и находить выход из него. А кроме того, помещенная в уже известный ей лабиринт, она не искала выход, а сразу же, не заглядывая в тупиковые ходы, выходила из лабиринта.

Американский кибернетик А. Самуэль составил для вычислительной машины программу, которая позволяет ей играть в шашки, причем в ходе игры машина обучается или, по крайней мере, создает впечатление, что обучается, улучшая свою игру на основе накопленного опыта. В 1962 г.
эта программа сразилась с Р. Нили, сильнейшим шашистом в США и победила.

Каким образом машине удалось достичь столь высокого класса игры?

Естественно, что в машину были программно заложены правила игры так, что выбор очередного хода был подчинен этим правилам. На каждой стадии игры машина выбирала очередной ход из множества возможных ходов согласно некоторому критерию качества игры. В шашках (как и в шахматах) обычно невыгодно терять свои фигуры, и, напротив, выгодно брать фигуры противника. Игрок (будь он человек или машина), который сохраняет подвижность своих фигур и право выбора ходов и в то же время держит под боем большое число полей на доске, обычно играет лучше своего противника, не придающего значения этим элементам игры. Описанные критерии хорошей игры сохраняют свою силу на протяжении всей игры, но есть и другие критерии, которые относятся к отдельным ее стадиям — дебюту, миттэндшпилю, эндшпилю.

Разумно сочетая такие критерии (например в виде линейной комбинации с экспериментально подбираемыми коэффициентами или более сложным образом), можно для оценки очередного хода машины получить некоторый числовой показатель эффективности — оценочную функцию. Тогда машина, сравнив между собой показатели эффективности очередных ходов, выберет ход, соответствующий наибольшему показателю. Подобная автоматизация выбора очередного хода не обязательно обеспечивает оптимальный выбор, но все же это какой-то выбор, и на его основе машина может продолжать игру, совершенствуя свою стратегию (образ действия) в процессе обучения на прошлом опыте. Формально обучение состоит в подстройке параметров (коэффициентов) оценочной функции на основе анализа проведенных ходов и игр с учетом их исхода.

По мнению А. Самуэля, машина, использующая этот вид обучения, может научиться играть лучше, чем средний игрок, за относительно короткий период времени.

Можно сказать, что все эти элементы интеллекта, продемонстрированные машиной в процессе игры в шашки, сообщены ей автором программы. Отчасти это так.


Но не следует забывать, что программа эта не является "жесткой", заранее продуманной во всех деталях. Она совершенствует свою стратегию игры в процессе самообучения. И хотя процесс "мышления" у машины существенно отличен оттого, что происходит в мозгу играющего в шашки человека, она способна у него выиграть.

Ярким примером сложной интеллектуальной игры до недавнего времени являлись шахматы. В 1974 г. состоялся международный шахматный турнир машин, снабженных соответствующими программами. Как известно, победу на этом турнире одержала советская машина с шахматной программой "Каисса".

Почему здесь употреблено "до недавнего времени"? Дело в том, что недавние события показали, что несмотря на довольно большую сложность шахмат, и невозможность, в связи с этим произвести полный перебор ходов, возможность перебора их на большую глубину, чем обычно, очень увеличивает шансы на победу. К примеру, по сообщениям в печати, компьютер фирмы IBM, победивший Каспарова, имел 256 процессоров, каждый из которых имел 4 Гб дисковой памяти и 128 Мб оперативной. Весь этот комплекс мог просчитывать более 100'000'000 ходов в секунду. До недавнего времени редкостью был компьютер, могущий делать такое количество целочисленных операций в секунду, а здесь мы говорим о ходах, которые должны быть сгенерированы и для которых просчитаны оценочные функции. Хотя с другой стороны, этот пример говорит о могуществе и универсальности переборных алгоритмов.

В настоящее время существуют и успешно применяются программы, позволяющие машинам играть в деловые или военные игры, имеющие большое прикладное значение. Здесь также чрезвычайно важно придать программам присущие человеку способность к обучению и адаптации. Одной из наиболее интересных интеллектуальных задач, также имеющей огромное прикладное значение, является задача обучения распознавания образов и ситуаций. Решением ее занимались и продолжают заниматься представители различных наук — физиологи, психологи, математики, инженеры.


Такой интерес к задаче стимулировался фантастическими перспективами широкого практического использования результатов теоретических исследований: читающие автоматы, системы ИИ, ставящие медицинские диагнозы, проводящие криминалистическую экспертизу и т. п., а также роботы, способные распознавать и анализировать сложные сенсорные ситуации.

В 1957 г. американский физиолог Ф. Розенблатт предложил модель зрительного восприятия и распознавания — перцептрон. Появление машины, способной обучаться понятиям и распознавать предъявляемые объекты, оказалось чрезвычайно интересным не только физиологам, но и представителям других областей знания и породило большой поток теоретических и экспериментальных исследований.

Перцептрон или любая программа, имитирующая процесс распознавания, работают в двух режимах: в режиме обучения и в режиме распознавания. В режиме обучения некто (человек, машина, робот или природа), играющий роль учителя, предъявляет машине объекты и о каждом их них сообщает, к какому понятию (классу) он принадлежит. По этим данным строится решающее правило, являющееся, по существу, формальным описанием понятий. В режиме распознавания машине предъявляются новые объекты (вообще говоря, отличные от ранее предъявленных), и она должна их классифицировать, по возможности, правильно.

Проблема обучения распознаванию тесно связана с другой интеллектуальной задачей — проблемой перевода с одного языка на другой, а также обучения машины языку. При достаточно формальной обработке и классификации основных грамматических правил и приемов пользования словарем можно создать вполне удовлетворительный алгоритм для перевода, скажем научного или делового текста. Для некоторых языков такие системы были созданы еще в конце 60-г. Однако для того, чтобы связно перевести достаточно большой разговорный текст, необходимо понимать его смысл. Работы над такими программами ведутся уже давно, но до полного успеха еще далеко. Имеются также программы, обеспечивающие диалог между человеком и машиной на урезанном естественном языке.



Что же касается моделирования логического мышления, то хорошей модельной задачей здесь может служить задача автоматизации доказательства теорем. Начиная с 1960 г., был разработан ряд программ, способных находить доказательства теорем в исчислении предикатов первого порядка. Эти программы обладают, по словам американского специалиста в области ИИ Дж. Маккатти, "здравым смыслом", т. е. способностью делать дедуктивные заключения.

В программе К. Грина и др., реализующей вопросно-ответную систему, знания записываются на языке логики предикатов в виде набора аксиом, а вопросы, задаваемые машине, формулируются как подлежащие доказательству теоремы. Большой интерес представляет "интеллектуальная" программа американского математика Хао Ванга. Эта программа за 3 минуты работы IBM-704 вывела 220 относительно простых лемм и теорем из фундаментальной математической монографии, а затем за 8.5 мин выдала доказательства еще 130 более сложных теорем, часть их которых еще не была выведена математиками. Правда, до сих пор ни одна программа не вывела и не доказала ни одной теоремы, которая бы, что называется "позарез" была бы нужна математикам и была бы принципиально новой.

Очень большим направлением систем ИИ является роботехника. В чем основное отличие интеллекта робота от интеллекта универсальных вычислительных машин?

Для ответа на этот вопрос уместно вспомнить принадлежащее великому русскому физиологу И. М. Сеченову высказывание: "… все бесконечное разнообразие внешних проявлений мозговой деятельности сводится окончательно лишь к одному явлению — мышечному движению". Другими словами, вся интеллектуальная деятельность человека направлена в конечном счете на активное взаимодействие с внешним миром посредством движений. Точно так же элементы интеллекта робота служат прежде всего для организации его целенаправленных движений. В то же время основное назначение чисто компьютерных систем ИИ состоит в решении интеллектуальных задач, носящих абстрактный или вспомогательный характер, которые обычно не связаны ни с восприятием окружающей среды с помощью искусственных органов чувств, ни с организацией движений исполнительных механизмов.



Первых роботов трудно назвать интеллектуальными. Только в 60-х годах появились очуствленные роботы, которые управлялись универсальными компьютерами. К примеру в 1969 г. в Электротехнической лаборатории (Япония) началась разработка проекта "промышленный интеллектуальный робот". Цель этой разработки — создание очуствленного манипуляционного робота с элементами искусственного интеллекта для выполнения сборочно-монтажных работ с визуальным контролем.

Манипулятор робота имеет шесть степеней свободы и управляется мини-ЭВМ NEAC-3100 (объем оперативной памяти 32000 слов, объем внешней памяти на магнитных дисках 273000 слов), формирующей требуемое программное движение, которое отрабатывается следящей электрогидравлической системой. Схват манипулятора оснащен тактильными датчиками.

В качестве системы зрительного восприятия используются две телевизионные камеры, снабженные красно-зелено-синими фильтрами для распознавания цвета предметов. Поле зрения телевизионной камеры разбито на 64*64 ячеек. В результате обработки полученной информации грубо определяется область, занимаемая интересующим робота предметом. Далее, с целью детального изучения этого предмета выявленная область вновь делится на 4096 ячеек. В том случае, когда предмет не помещается в выбранное "окошко", оно автоматически перемещается, подобно тому, как человек скользит взглядом по предмету. Робот Электротехнической лаборатории был способен распознавать простые предметы, ограниченные плоскостями и цилиндрическими поверхностями при специальном освещении. Стоимость данного экспериментального образца составляла примерно 400000 долларов.

Постепенно характеристики роботов монотонно улучшались, Но до сих пор они еще далеки по понятливости от человека, хотя некоторые операции уже выполняют на уровне лучших жонглеров. К примеру удерживают на лезвии ножа шарик от настольного тенниса.

Еще пожалуй здесь можно выделить работы киевского Института кибернетики, где под руководством Н. М. Амосова и В. М. Глушкова (ныне покойного) ведется комплекс исследований, направленных на разработку элементов интеллекта роботов.


Особое внимание в этих исследованиях уделяется проблемам распознавания изображений и речи, логического вывода (автоматического доказательства теорем) и управления с помощью нейроподобных сетей.

К примеру можно рассмотреть созданный еще в 70-х годах макет транспортного автономного интегрального робота (ТАИР). Конструктивно ТАИР представляет собой трехколесное шасси, на котором смонтирована сенсорная система и блок управления. Сенсорная система включает в себя следующие средства очуствления: оптический дальномер, навигационная система с двумя радиомаяками и компасом, контактные датчики, датчики углов наклона тележки, таймер и др. И особенность, которая отличает ТАИР от многих других систем, созданных у нас и за рубежом, это то, что в его составе нет компьютера в том виде, к которому мы привыкли. Основу системы управления составляет бортовая нейроподобная сеть, на которой реализуются различные алгоритмы обработки сенсорной информации, планирования поведения и управления движением робота.

В конце данного очень краткого обзора рассмотрим примеры крупномасштабных экспертных систем.

MICIN — экспертная система для медицинской диагностики. Разработана  группой по инфекционным заболеваниям Стенфордского университета. Ставит соответствующий диагноз, исходя из представленных ей симптомов, и рекомендует курс медикаментозного лечения любой из диагностированных инфекций. База данных состоит из 450 правил.

PUFF — анализ нарушения дыхания. Данная система представляет собой MICIN, из которой удалили данные по инфекциям и вставили данные о легочных заболеваниях.

DENDRAL — распознавание химических структур. Данная система старейшая, из имеющих звание экспертных. Первые версии данной системы появились еще в 1965 году во все том же Стенфордском университете. Пользователь дает системе DENDRAL некоторую информацию о веществе, а также данные спектрометрии (инфракрасной, ядерного магнитного резонанса и масс-спектрометрии), и та в свою очередь выдает диагноз в виде соответствующей химической структуры.

PROSPECTOR — экспертная система, созданная для содействия поиску коммерчески оправданных месторождений полезных ископаемых.

Язык Рефал

Название языка происходит от "РЕкурсивных Функции АЛгоригми-ческий язык". Нас будут также интересовать соображения, которые привели к построению этого языка — эти соображения имеют на наш взгляд весьма общий характер и полезны для лучшего понимания причин возникновения продукционного подхода в программировании.

Разработчики языка Рефал делят алгоритмические языки на две группы. Первую группу образуют языки, которые называются языки операторного, или процедурного типа. Элементарными единицами программы являются здесь операторы, т.е. приказы, выполнение которых сводится к четко оп­ределенному изменению четко определенной части памяти машины. Ти­пичным представителем этой группы является язык машины Поста. Сюда же относятся машинные языки конретных ЭВМ, а также массовые языки программирования типа Фортран, Алгол, ПЛ/1.

Языки второй группы называются языками сентенциального, или дек­ларативного типа (sentence — высказывание, предложение). Программа на таком языке представляется в виде набора предложений (соотношений, правил, формул), которые машина, понимающая данный язык, умеет каким-то образом применять к обрабатываемой информации. Простей­шим примером сентенциального языка, созданного с теоретическими це­лями является язык нормальных алгоритмов Маркова.

Можно указать прообразы указанных типов алгоритмических языков в естественных языках. Для операторных языков это повелительное накло­нение (императив, приказание), для сентенциалышх - изъявительное нак­лонение (описание, повествование). Обращаясь к естественному языку, нетрудно заметить, что "изъявительное наклонение является несравненно более распространенным и образует, в сущности, основу языка, в то время как повелительное наклонение предстает в виде некоторой специальной модификации". Таким образом, можно сделать вывод о том, что "относительный вес изъявительного наклонения является мерой развитос­ти языка".

Язык РЕФАЛ является сентенциальным в своей основе, а вся информа­ция в этом языке представляется в виде правил конкретизации.
Каждое правило записывается в виде предложения, которое представляет собой продукцию с определенными синтаксисом и семантикой. Предложения в Рефал-программе отделяются друг от друга знаком § (параграф).

Каждое правило конкретизации определяет раскрытие смысла некото­рого понятия через более элементарные. Операцию конкретизации можно также определить как переход от имени к значению. Введем два знака:

k и ^, которые будем называть конкретизационными скобками, и кото­рые будут содержать объект, подлежащий конкретизации. Так, если х — некоторая переменная, то kx^. (конкретизация х) будет изображать значе­ние этой величины. Другой пример: объект k28 +7^ при правильном опре­делении операции сложения рано или поздно будет заменен на объект 35.

Выполнение конкретизации — переход от имени к значению — объявляется основной и, по существу, единственной операцией в языке Рефал. Эту опера­цию будет выполнять Рефал-машина (имеется в виду машина на логи­ческом уровне, имитируемая соответствующим транслятором на уни­версальной ЭВМ; возможно, разумеется, и построение реальной "физи­ческой" Рефал-машины).

Поскольку правило конкретизации есть указание для замены одного объекта (слова в некотором алфавите) на другой, предложения языка Рефал должны состоять из левой части (заменяемый объект) и правой части (объект, заменяющий левую часть). Для разделения правой и левой части мы будем использовать знак стрелки "à".

Пример 3.5. Предложение, выражающее тот факт, что значение переменной Х есть 137, записывается в виде

§kX^à137.

Между знаком § и первым знаком k можно вставлять последовательность знаков, которая будет служить номером предложения, или комментарием к нему, например:

§ l.l kX^à137.                                                                                                    

(ф.  27)

Опишем теперь структуру Рефал-машины, которая, используя предло­жения Рефал-программы, будет выполнять конкретизации.


Будем считать, что объектом обработки является некоторое выражение (слово), которое находится в поле зрения машины. Работа машины осуществляется по шагам, каждый из которых представляет выполнение одного акта, конкрети­зации.

Пусть программа машины состоит из единственного предложения (ф.  27), а в поле зрения находится выражение kX^. Тогда за один шаг машина заме­нит содержимое поле зрения на 137, после чего она остановится, т. к. знаков конкретизации больше нет, и следовательно, делать ей больше нечего.

Так как Рефал-программа содержит, вообще говоря, набор (последова­тельность) предложений, может оказаться, что для выполнения данной кон­кретизации пригодно не одно, а несколько предложений. Например, в поле памяти, кроме (ф.  27), может находиться еще предложение

§ 1.2 kX^à274.

Неоднозначность, которая отсюда может возникнуть, устраняется так же, как это принято в нормальных алгоритмах Маркова (читатель, видимо, уже заметил, что Рефал-машина следует идеологии этих алгоритмов): машина просматривает предложения в том порядке, в котором они рас­положены в Рефал-программе, и применяет первое из них, которое окажет­ся подходящим.

Поле зрения может содержать сколько угодно конкретизационных ско­бок, причем они могут быть как угодно вложены друг в друга. В этом случае Рефал-машина начинает процесс конкретизации с первого из зна­ков k, в области действия которого (т.е. в последовательности знаков до парной скобки ^) нет ни одного знака k. Выражение, находящееся в об­ласти этого знака k, последовательно. сравнивается с левыми частями предложений Рефал-программы. Найдя подходящее предложение, машина выполняет в поле зрения необходимую замену и переходит к следующе­му шагу конкретизации.

Пример. Пусть Рефал-программа имеет вид

kX^à137

kX^à274

kY^à2

k137+2^à139,

а поле зрения содержит выражение

kkX^+kY^^.

На первом шаге замене подлежит подвыражение kX^ — получим в поле зрения kl37 + kY^^. Теперь в первую очередь конкретизируется kY^ — получим в результате применения третьего предложения k137 +2^ и на последнем шаге получим 139, не содержащее символов k. (Разумеется для реального сложения используются соответствующие встроенные функции, а этот пример — лишь простейшая иллюстрация принципов рабо­ты машины [21]).



Чтобы иметь возможность представлять обобщенные предложения, ис­пользуются три типа переменных: е — для представления выражений; t — для термов; s — для символов. В простейшем случае переменные записы­ваются в виде указателя типа (е, t, s) и индекса; например, е1, e2 — пере­менные, пробегающие в качестве значений выражения. Выражением в язы­ке Рефал называется последовательность знаков, правильно построенная в соответствеии с синтаксисом языка Рефал. Терм языка Рефал — это либо символ, либо выражение в круглых или конкретизационных скобках. Выражения строятся из термов.

Пример. Предположим, требуется написать программу, кото­рая выполняет раскрытие скобок в алгебраических выражениях, построен­ных из букв с помощью скобок, знаков сложения "+" и умножения"*". Рассмотрим процесс написания такой программы. Если некоторое выра­жение е имеет вид е1 + e1, где е1, e1 — выражения, то для раскрытия ско­бок надо: раскрыть скобки в e1, раскрыть скобки в е2, полученные резуль­таты сложить. Эту мысль в компактном, но в то же время и наглядном ви­де выражает предложение:

§ 2.1 ke1 +e2^à ke1^ +ke2^

Если же выражение е имеет вид e1 * e2, то, вообще говоря, необходимо учитывать две возможности:

— хотя бы один из сомножителей есть сумма (например, е = (А + В) *С),

— ни одно из выражений е1 или е2 не представимо в виде суммы (на­пример, е = (А * В) * (С * Л)).

В первом случае надо описать законы дистрибутивности:

§ 2.2ke1 * (e2 +e3) ^àke1 * e2^ +ke1*e3^,

§ 2.3k(e1 +e2) * e3^àke1 * e3^  + ke2*e3^ ,

§ 2.4ke1 * (e2 + e3) * e4 ^ à k(e1 * е2 + e1 * e3) * e4^.

Во втором случае по аналогии со сложением имеем

§ 2.5ke1 * е2^ à ke1^* ke2^.

Наконец, осталось выразить возможность "снятия внешних скобок" и условие "терминальности" символов, что определяют предложения:

§ 2.6k(e) ^ à ke^,

§ 2.7ks^ à s

(буквы не подлежат конкретизации).

Приведенные семь предложений § 2.1 - § 2.7 решают задачу.


Рассмот­ рим как эта программа обрабатывает выражение

k(A +B) * (С +D) ^.

Последовательно получим в результате работы программы (для удобства слева указываем номер правила, которое непосредственно привело к дан­ному выражению):

§2.2 k(A +В)*С^. + k(A +B)*D^,

§2.3 kA *C^ +kB*C^ + k(A+B)*D^,

§2.3 kA *C^ + kB*C^ + kA *D^ + kB*D^.

Далее ограничимся рассмотрением первого слагаемого:

§ 2.5 kA^ * kC^ + ...,

§2.7 A * kC^ + ...,

§ 2.7 А * С + ... .

После аналогичной обработки остальных слагаемых получим искомое выражение

А*С+D*С+А * D + В * D.

Если на вход поступит выражение

kA + (B + С) ^,

то получим последовательно:

§ 2.1 kA^ + k(B + С) ^,

§ 2.7 А + k (Д + С) ^,

§ 2.6 А + kB + C^,

§2.1, 2.7 A + B + С.

Обратите внимание, что если расположить правило § 2.5 перед правила­ми § 2.2 и § 2.3, то придем к абсурду! Например, выражение А *(В+С) будет приведено к виду: А *В + С.

Элементы нечеткой логики

Как известно, классическая логика оперирует только с двумя значениями: истина и ложь. Однако этими двумя значениями довольно сложно представить (можно, но громоздко) большое количество реальных задач. Поэтому для их решения был разработан специальный математический аппарат, называемый нечеткой логикой. Основным отличием нечеткой логики от классической, как явствует из названия, является наличие не только двух классических состояний (значений), но и промежуточных:

FÎ{0…1}

Соответственно, вводятся расширения базовых операций логического умножения, сложения и отрицания (сравните с соответствующими операциями теории вероятностей):

Как можно легко заметить, при использовании только классических состояний (ложь-0, истина-1) мы приходим с классическим законам логики.

Нечеткое логическое управление может использоваться, чтобы осуществлять разнообразные интеллектуальные функции, в самых разнообразных электронных товарах и домашних приборах, к авто электронике, управлению производственными процессами и автоматизации.

Кластерный анализ

Кластерный анализ предназначен для разбиения множест­ва объектов на заданное или неизвестное число классов на основании некоторого математического критерия качества классификации (cluster (англ.) — гроздь, пучок, скопление, группа элементов, характеризуемых каким-либо общим свой­ством). Критерий качества кластеризации в той или иной мере отражает следующие неформальные требования:

а) внутри групп объекты должны быть тесно связаны между собой;

б) объекты разных групп должны быть далеки друг от друга;

в) при прочих равных условиях распределения объектов по группам должны быть равномерными.

Требования а) и б) выражают стандартную концепцию ком­пактности классов разбиения; требование в) состоит в том, чтобы критерий не навязывал объ­единения отдельных групп объектов.

Узловым моментом в кластерном анализе считается выбор метрики (или меры близости объектов), от которого решающим образом зависит окончательный вариант разбиения объектов на группы при заданном алгоритме разбиения. В каждой конкретной задаче этот выбор произво­дится по-своему, с учетом главных целей исследования, физи­ческой и статистической природы используемой информации и т. п. При применении экстенсиональных методов распозна­вания, как было показано в предыдущих разделах, выбор метрики достигается с помощью специальных алгоритмов преобразования исходного пространства признаков.

Другой важной величиной в кластерном анализе является расстояние между целыми группами объектов. Приведем примеры наиболее распространенных расстояний и мер близости, характеризующих взаимное расположение отдельных групп объектов. Пусть wi — i-я группа (класс, кластер) объектов, Ni — число объектов, образующих группу wi, вектор mi — среднее арифме­тическое объектов, входящих в wi (другими словами [mi — «центр тяжести» i-й группы), a q ( wl, wm ) — расстояние меж­ду группами wl и wm

Рис.  11. Различные способы определения расстояния между кластерами wl и wm: 1 — по центрам тяжести, 2 — по ближайшим объектам, 3 — по самым далеким объектам

Рис. 3.11.

Расстояние ближайшего соседа есть расстояние между бли­жайшими объектами кластеров:



 Расстояние дальнего соседа — расстояние между самыми дальними объектами кластеров:

 

Расстояние центров тяжести равно расстоянию между центральными точками кластеров:

 

Обобщенное (по Колмогорову) расстояние между классами, или обобщенное K-расстояние, вычисляется по формуле



В частности, при t à µ и при t à -µ имеем





Выбор той или иной меры расстояния между кластерами влияет, главным образом, на вид выделяемых алгоритмами кла­стерного анализа геометрических группировок объектов в пространстве признаков. Так, алгоритмы, основанные на расстоянии ближайшего соседа, хорошо работают в случае группировок, имеющих сложную, в частности, цепочечную структуру. Расстояние дальнего соседа применяется, когда ис­комые группировки образуют в пространстве признаков шаровидные облака. И промежуточное место занимают ал­горитмы, использующие расстояния центров тяжести и средней связи, которые лучше всего работают в случае группировок эл­липсоидной формы.

Нацеленность алгоритмов кластерного анализа на опре­деленную структуру группировок объектов в пространстве признаков может приводить к неоптимальным или даже неправильным результатам, если гипотеза о типе группировок неверна. В случае отличия реальных распределений от ги­потетических указанные алгоритмы часто «навязывают» дан­ным не присущую им структуру и дезориентируют исследо­вателя. Поэтому экспериментатор, учитывающий данный факт, в условиях априорной неопределенности прибегает к применению батареи алгоритмов кластерного анализа и от­дает предпочтение какому-либо выводу на основании комп­лексной оценки совокупности результатов работы этих ал­горитмов.

Алгоритмы кластерного анализа отличаются большим разнообразием. Это могут быть, например, алгоритмы, реализу­ющие полный перебор сочетаний объектов или осуществляю­щие случайные разбиения множества объектов.


В то же время большинство таких алгоритмов состоит из двух этапов. На первом этапе задается начальное (возможно, искусственное или даже произвольное) разбиение множества объектов на классы и определяется некоторый математический критерий качества автоматической классификации. Затем, на втором этапе, объек­ты переносятся из класса в класс до тех пор, пока значение критерия не перестанет улучшаться.

Многообразие алгоритмов кластерного анализа обусловле­но также множеством различных критериев, выражающих те или иные аспекты качества автоматического группирования. Простейший критерий качества непосредственно базируется на величине расстояния между кластерами. Однако такой критерий не учитывает «населенность» кластеров — относи­тельную плотность распределения объектов внутри выделяе­мых группировок. Поэтому другие критерии основываются на вычислении средних расстояний между объектами внутри кла­стеров. Но наиболее часто применяются критерии в виде от­ношений показателей «населенности» кластеров к расстоянию между ними. Это, например, может быть отношение суммы межклассовых расстояний к сумме внутриклассовых (между объектами) расстояний или отношение общей дисперсии дан­ных к сумме внутриклассовых дисперсий и дисперсии центров кластеров.

Функционалы качества и конкретные алгоритмы автомати­ческой классификации достаточно полно и подробно рассмот­рены в специальной литературе. Эти функционалы и ал­горитмы характеризуются различной трудоемкостью и подчас требуют ресурсов высокопроизводительных компьютеров. Раз­нообразные процедуры кластерного анализа входят в состав практически всех современных пакетов прикладных программ для статистической обработки многомерных данных.

Коллективы решающих правил

Давно известны приемы повышения качества принимаемых реше­ний, состоящие в объединении специалистов той или иной области знаний в коллектив, вырабатывающий совместное решение. Идею коллективного решения можно применить и к «коллективу» фор­мальных алгоритмов, что позволит повысить эффективность ре­шения многих задач.

Для рационального использования особенностей различных алгоритмов при решении задач распознавания возможно объединить различные по характеру алгоритмы распозна­вания в коллективы, формирующие классификационное решение на основе правил, принятых в теории коллективных решений. Пусть в некоторой ситуации Х принимается решение S. Тогда S=R(X), где R—алгоритм принятия решения в ситуации X. Предположим, что существует L различных алгоритмов решения задачи, т. е. Sl=Rl(X), l=1, 2, ... , L, где Sl—решение, получен­ное алгоритмом Rl. Будем называть множество алгоритмов {R}={R1, R2, ..., Ri.} коллективом алгоритмов решения задачи (кол­лективом решающих правил), если на множестве решений Sl в любой ситуации Х определено решающее правило F, т. е. S=F(S1, S2, ..., SL, X). Алгоритмы Rl принято называть членами коллектива, Sl — решением l-го члена коллектива, а S — коллек­тивным решением. Функция F определяет способ обобщения ин­дивидуальных решений в решения коллектива S. Поэтому синтез функции F, или способ обобщения, является центральным момен­том в организации коллектива.

Принятие коллективного решения может быть использовано при решении различных задач. Так, в задаче управления под си­туацией понимается ситуация среды и целей управления, а под решением — самоуправление, приводящее объект в целевое состоя­ние. В задачах прогноза Х — исходное, а S — прогнозируемое состояние. В задачах распознавания ситуацией Х является опи­сание объекта X, т. е. его изображение, а решением S — номер образа, к которому принадлежит наблюдаемое изображение. Индивидуальное и коллективное решения в задаче распозна­вания состоят в отнесении некоторого изображения к одному из образов.
Наиболее интересными коллективами распознающих ал­горитмов являются такие, в которых существует зависимость веса каждого решающего правила Rl от распознаваемого изображения. Например, вес решающего правила Rl может определяеться соотно­шением

                                                                                                (ф.  25)

 где Bl — область компетентности решающего правила Rl. Веса решающих правил выбираются так, что

                                                                                                                     (ф.  26)

для всех возможных значений X. Соотношение (ф.  25) означает, что решение коллектива определяется решением того решающего правила Ri, области компетентности которого принадлежит изоб­ражение объекта X. Такой подход представляет собой двухуров­невую процедуру распознавания. На первом уровне определяется принадлежность изображения той или иной области компетент­ности, а уже на втором — вступает в силу решающее правило, компетентность которого максимальна в найденной области. Решение этого правила отождествляется с решением всего кол­лектива. Основным этапом в такой организации коллективного решения является обучение распознаванию областей компетентности. Прак­тически постановкой этой задачи различаются правила органи­зации решения коллектива. Области компетентности можно ис­кать, используя вероятностные свойства правил коллектива, можно применить гипотезу компактности и считать, что одина­ковым правилам должны соответствовать компактные области, которые можно выделить алгоритмами самообучения. В про­цессе обучения сначала выделяются компактные множества и соответствующие им области, а затем в каждой из этих областей восстанавливается свое решающее правило. Решение такого пра­вила, действующего в определенной области, объявляется дикта­торским, т. е. отождествляется с решением всего коллектива.

В перцептроне каждый A-элемент может интерпретироваться как член коллектива.В процессе обучения все A-элементы при­обретают веса, в соответствии с которыми эти A-элементы участ­вуют в коллективном решении. Особенность каждого A-элемента состоит в том, что он действует в некотором подпространстве ис­ходного пространства, характер которого определяется связями между S- и A-элементами. Решение, получаемое на выходе перцептрона, можно интерпретировать как средневзвешенное реше­ние коллектива, состоящего из всех A-элементов.

КОНСТАНТЫ

Константы известны всем программистам. В Прологе константа может быть атомом или числом.

Лекции 4-7: Системы распознавания образов (идентификации)

Понятие образа. Проблема обучения распознаванию образов. Геометрический и структурный подходы. Гипотеза компактности. Обучение и самообучение. Адаптация и обучение.

Методы обучения распознаванию образов - перцептроны, нейронные сети, метод потенциальных функций, метод группового учета аргументов, метод предельных упрощений, коллективы решающих правил.

Методы и алгоритмы анализа структуры многомерных данных - кластерный анализ, иерархическое группирование.

Лекционные занятия - 8 ч.

Практика - 4 ч.

Лекции 8-11. Логический подход к построению систем ИИ

Представление в компьютере неформальных процедур. Языки логического программирования Рефал, Пролог, К-системы.

Элементы нечеткой логики.

Лекционные занятия - 8 ч.

Практика - 2 ч.

Лекция 3: Архитектура и основные составные части систем ИИ

Различные подходы к построению систем ИИ (логический, структурный, эволюционный, имитационный) и методы представления знаний. Краткое ознакомление с данными подходами. Вспомогательные системы (распознавание образов зрительных и звуковых, идентификация, моделирование, жесткое программирование) и их место в системах ИИ.

Лекционные занятия - 2 ч.

Логический вывод

Важность логического вывода становится очевидной уже при рассмотрении простейших информационно-логических процедур. Предположим, что некоторая база данных содержит сведения об отношениях "õ — ОТЕЦ у" и "х — МАТЬ у". Чтобы обработать запросы типа:

ИВАНОВ А.И. — ДЕД ПЕТРОВА В.А.?

ПЕТРОВ В.А. — ВНУК ИВАНОВА А.И.?

необходимо либо ввести в базу данных также и сведения об отношениях "х — ДЕД у" и "х — ВНУК у", либо объяснить системе, как из отношений ОТЕЦ, МАТЬ извлечь искомую информацию. Реализация первой возможности связана с неограниченным ростом избыточности базы данных. Вторая возможность при традиционном алгоритмическом подходе требует написания все новых и новых программ для реализации новых типов запросов.

Логический вывод позволяет расширять возможности "общения" наиболее просто и наглядно. Так, для приведенных типов запросов системе достаточно будет сообщить три правила:

1. х—ДЕД у если х—ОТЕЦ а и а—РОДИТЕЛЬ у

2. х—РОДИТЕЛЬ у если х—ОТЕЦ у или х—МАТЬ у

3. х—ВНУК у если у—ДЕД х

Эти правила содержат естественные и очевидные определения понятий ДЕД, РОДИТЕЛЬ, ВНУК. Поясним в чем состоит логический вывод для запроса "А—ДЕД В?" в предположении, что в базе данных имеются факты: А—ОТЕЦ Б и Б—МАТЬ В. При этом для упрощения опустим тонкости, связанные с падежными окончаниями. Пользуясь определением 1 система придет к необходимости проверки существования такого индивидуума а, что факты А—ОТЕЦ а и а—РОДИТЕЛЬ В истинны. Если такой а существует, то А—ДЕД В, если не существует такого а, то А не является дедом В.

Механизм возврата

При попытке согласования целевого утверждения Пролог выби­рает первое из тех утверждений, голова которых сопоставима с целе­вым утверждением. Если удастся согласовать тело утверждения, то целевое утверждение согласовано. Если нет, то Пролог переходит к следующему утверждению, голова которого сопоставима с целевым утверждением, и так далее до тех пор, пока целевое утверждение не будет согласовано или не будет доказано, что оно не согласуется с ба­зой данных.

В качестве примера рассмотрим утверждения:

меньше(X.Y) :-

XY, write(X),

write ('меньше, чем'),write(Y).

меньше(Х.У) :-

XY, write(Y),

write ('меньше, 4CM'),write(X).

Целевое утверждение

?- меньше (5, 2).

сопоставляется с головой первого утверждения при Х=5 и У=2. Одна­ко не удается согласовать первый член конъюнкции в теле утвержде­ния X<Y. Значит, Пролог нс может использовать первое утвержде­ние для согласования целевого утверждения меньше(5, 2). Тогда Пролог переходит к следующему утверждению, голова которого со­поставима с целевым утверждением. В нашем случае это второе утверждение. При значениях переменных Х=5 и Y=2 тело утверждения согласуется. Целевое утверждение меньше(5,2) доказано, и Пролог выдает сообщение «2 меньше, чем 5». Запрос

?-меньше (2, 2).

сопоставляется с головой первого утверждения, но тело утверждения согласовать не удается. Затем происходит сопоставление с головой второго утверждения, но согласовать тело опять-таки оказывается невозможно. Поэтому попытка доказательства целевого утвержде­ния меньше(2, 2) заканчивается неудачей.

Такой процесс согласования целевого утверждения путем прямого продвижения по программе мы называем прямой трассировкой (forward tracking). Даже если целевое утверждение согласовано, с помощью прямой трассировки мы можем попытаться получить другие варианты его доказательства, т.е. вновь согласовать целевое утверждение.

Пролог производит доказательство конъюнкции целевых утверж­дений слева направо. При этом может встретиться целевое утвержде­ние, согласовать которое не удается. Если такое случается, то проис­ходит смещение влево до тех пор, пока не будет найдено целевое ут­верждение, которое может быть вновь согласовано, или не будут ис черпаны все предшествующие целевые утверждения. Если слева нет целевых утверждений, то конъюнкцию целевых утверждений согласовать нельзя. Однако, если предшествующее целевое утверждениг может быть согласовано вновь, Пролог возобновляет процесс доказа­тельства целевых утверждений слева направо, начиная со следующе­го справа целевого утверждения. Описанный процесс смещения вле­во для повторного согласования целевого утверждения и возвраще­ния вправо носит название механизма возврата.

Механизм возврата и процедурная семантика

При согласовании целевого утверждения в Прологе используется метод, известный под названием механизма возврата. В этой главе мы показываем, в каких случаях применяется механизм возврата, как он работает и как им пользоваться. Описывается декларативная и процедурная семантика процедур Пролога. Завершается глава об­суждением вопросов эффективности.

Метод наименьших квадратов

Перед тем, как начинать рассмотрение МГУА, было бы полезно вспомнить или узнать впервые метод наименьших квадратов — наиболее распространенный метод подстройки линейно зависимых параметров.

Рассмотрим для примера МНК для трех аргументов:

Пусть функция T=T(U, V, W) задана таблицей, то есть из опыта известны числа U­i, Vi, Wi, Ti ( i = 1, … , n). Будем искать зависимость между этими данными в виде:

                                                                                   (ф.  11)

где a, b, c — неизвестные параметры.

Подберем значения этих параметров так, чтобы была наименьшей сумма квадратов уклонений опытных данных Ti и теоретических Ti = aUi + bVi + cWi, то есть сумма:

                                                               (ф.  12)

Величина s является функцией трех переменных a, b, c. Необходимым и достаточным условием существования минимума этой функции является равенство нулю частных производных функции s по всем переменным, то есть:

                                                                                    (ф.  13)

Так как:

                                                                  (ф.  14)

то система для нахождения a, b, c будет иметь вид:

                                                         (ф.  15)

Данная система решается любым стандартным методом решения систем линейных уравнений (Гаусса, Жордана, Зейделя, Крамера).

Рассмотрим некоторые практические примеры нахождения приближающих функций:

  y = ax2 + bx + g

Задача подбора коэффициентов a, b, g сводится к решению общей задачи при T=y, U=x2, V=x, W=1, a=a, b=b, g=c.

  f(x, y) = asin(x) + bcos(y) + g/x

Задача подбора коэффициентов a, b, g сводится к решению общей задачи при T=f, U=sin(x), V=cos(y), W=1/x, a=a, b=b, g=c.

Если мы распространим МНК на случай с m параметрами,

                                                                               (ф.  16)

то путем рассуждений, аналогичных приведенным выше, получим следующую систему линейных уравнений:

                                                                (ф.  17)

где

,

Метод потенциальных функций

Предположим, что требуется разделить два непересекающихся образа V1 и V2. Это значит, что в пространстве изображений существует, по крайней мере, одна функция, которая полностью разделяет множества, соответствующие образам V1 и V2. Эта функция должна принимать положительные значения в точках, соответствующих объектам, принадлежащим образу V1, и отрицательные — в точках образа V2. В общем случае таких разделяющих функций может быть много, тем больше, чем компактней разделяемые множества. В процессе обучения требуется построить одну из этих функций, иногда в некотором смысле наилучшую.

Метод потенциальных функций связан со следующей процедурой. В процессе обучения с каждой точкой пространства изображений, соответствующей единичному объекту из обучающей последовательности, связывается функция U(X, Xi), заданная на всем пространстве и зависящая от Xi как от параметра. Такие функции называются потенциальными, так как они напоминают функции потенциала электрического поля вокруг точечного электрического заряда. Изменение потенциала электрического поля по мере удаления от заряда обратно пропорционально квадрату расстояния. Потенциал, таким образом, может служить мерой удаления точки от заряда. Когда поле образовано несколькими зарядами, потенциал в каждой точке этого поля равен сумме потенциалов, создаваемых в этой точке каждым из зарядов. Если заряды, образующие поле, расположены компактной группой, потенциал поля будет иметь наибольшее значение внутри группы зарядов и убывать по мере удаления от нее.

Обучающей последовательности объектов соответствует последовательность векторов X1, X2, …, в пространстве изображений с которыми связана последовательность U(X, X1), U(X, X2), … потенциальных функций, используемых для построения функций f(X1, X2, …). По мере увеличения числа объектов в процессе обучения функция f должна стремиться к одной из разделяющих функций. В результате обучения могут быть построены потенциальные функции для каждого образа:

,               ,                              (ф.  3)

В качестве разделяющей функции f(X) можно выбрать функцию вида:

,                                                                                          (ф.  4)

которая положительна для объектов одного образа и отрицательна для объектов другого.

В качестве потенциальной функции рассмотрим функцию вида

,

                                                (ф.  5)

где jj(X) — линейно независимая система функций; lj — действительные числа, отличные от нуля для всех j = 1, 2, … ; Xi — точка, соответствующая i-му объекту из обучающей последовательности. Предполагается, что jj(X) и U(X, Xi) ограничены при XÎV1 È V2; yj(X)=ljjj(X).

В процессе обучения предъявляется обучающая последовательность и на каждом n-м такте обучения строится приближение fn(X) характеризуется следующей основной рекуррентной процедурой:

,                                                                      (ф.  6)

Разновидности алгоритмов потенциальных функций отличаются выбором значений qn и rn, которые являются фиксированными функциями номера n. Как правило, qnº1, а rn выбирается в виде:

,                                                                                 (ф.  7)

где S(fn, f) — невозрастающие функции, причем

                                                                     (ф.  8)

Коэффициенты gn представляют собой неотрицательную числовую последовательность, зависящую только от номера n. Кроме того,  и  (например, gn=1/n) или gn=const.

Разработано несколько вариантов алгоритмов потенциальных функций, различие между которыми состоит в выборе законов коррекции разделяющей функции от шага к шагу, т. е. в выборе законов коррекции разделяющей функции от шага к шагу, т. е. в выборе коэффициентов rn. Приведем два основных алгоритма потенциальных функций.

1. Будем считать, что f0(X)º0 (нулевое приближение). Пусть в результате применения алгоритма после n-го шага построена разделяющая функция fn(X), а на (n+1)-м шаге предъявлено изображение Xn+1, для которого известно действительное значение разделяющей функции f(Xn+1).


Тогда функция fn+1(X) строится по следующему правилу:

             (ф.  9)

2. Во втором алгоритме также принимается, что f0(X)º0. Переход к следующему приближению, т. е. переход от функции fn(X) к fn+1(X), осуществляется в результате следующей рекуррентной процедуры:

                        (ф.  10)

где l — произвольная положительная константа, удовлетворяющая условию l=(1/2)×max(X, Xi).

Если в (ф.  5) принять

,

и предположить, что xv может иметь только два значения 0 и 1, то в этом случае алгоритм потенциальных функций будет совпадать со схемой перцептрона с индивидуальными порогами А-элементов и с коррекцией ошибок. Поэтому многие теоретические положения метода потенциальных функций могут быть успешно применены для анализа некоторых перцептронных схем.

Метод предельных упрощений (МПУ)

По тому, как организован процесс обучения распознающих систем, четко выделяются два подхода к проблеме ОРО. Первый основан на построении сложных разделяющих поверхностей в случайно выбранных пространствах, а во втором — центр тяжести проблемы переносится на достижение понимания принципов формирования такого описания объектов, в рамках которого сам процесс распознавания чрезвычайно прост. Обучение в этом случае рассматривается как некий процесс конструирования пространств для решения конкретных задач.

В МПУ предполагается, что разделяющая функция задается заранее в виде линейного (самого простого) полинома, а процесс обучения состоит в конструировании такого пространства минимальной размерности, в котором заранее заданная наиболее простая разделяющая функция безошибочно разделяет обучающую последовательность. МПР назван так потому, что в нем строится самое простое решающее правило в пространстве небольшой размерности, т. е. в простом пространстве.

Пусть на некотором множестве объектов V заданы два подмножества V*1 и V*2, определяющих собой образы на обучающей последовательности V. Рассмотрим i-е свойство объектов, такое, что некоторые объекты обучающей последовательности этим свойством обладают, а другие — нет. Пусть заданным свойством обладают объекты, образующие подмножество V1i, а объекты подмножества V2i этим свойством не обладают (V1i È V2i = V). Тогда i-е свойство называют признаком первого типа относительно образа V*1, если выполняются соотношения

 и

                                                                                                (ф.  18)

и признаком второго типа, если выполняются

 и                                                                                              (ф.  19)

Если же выполняются соотношения

 и                                                                                            (ф.  20)

то i-е свойство считается признаком первого типа относительно образа V*2, а если выполняются

 и

                                                                                                (ф.  21)

то это же свойство объявляется признаком второго типа относительно образа V*2. Если свойство не обладает ни одной из приведенных особенностей, то оно вообще не относится к признакам и не участвует в формировании пространства.

Одинаковые признаки — это два признака xi и xj, порождающие подмножества V1j, V2j, V1i, V2i, такие, что

V1j= V1i и V2j= V2i.                                                                                                 (ф.  22)

Доказано утверждение, смысл которого заключается в том, что если пространство конструировать из однотипных, но неодинаковых признаков, то в конце концов будет построено такое пространство, в котором обучающая последовательность будет безошибочно разделена на два образа линейным, т. е. самым простым, решающим правилом.

Метод предельных упрощений состоит в том, что в процессе обучения последовательно проверяются всевозможные свойства объектов и из них выбираются только такие, которые обладают хотя бы одной из особенностей, определяемых соотношениями (ф.  18), (ф.  21). Такой отбор однотипных, но неодинаковых признаков продолжается до тех пор, пока при некотором значении размерности пространства не наступит безошибочное линейное разделение образов на обучающей последовательности. В зависимости от того, из признаков какого типа строится пространство, в качестве разделяющей плоскости выбирается плоскость, описываемая уравнением

                                                                                                      (ф.  23)

либо уравнением

                                                                                                                     (ф.  24)

Каждый объект относится к одному из образов в зависимости от того, по какую сторону относительно плоскости находится соответствующий этому объекту вектор в пространстве признаков размерности n.

Модель нейронной сети с обратным распространением ошибки (back propagation)

В 1986 году Дж. Хинтон и его коллеги опубликовали статью с описанием модели нейронной сети и алгоритмом ее обучения, что дало новый толчок исследованиям в области искусственных нейронных сетей.

Нейронная сеть состоит из множества одинаковых элементов — нейронов, поэтому начнем с них рассмотрение работы искусственной нейронной сети.

Биологический  нейрон моделируется как устройство, имеющее несколько входов (дендриты), и один выход (аксон). Каждому входу ставится в соответствие некоторый весовой коэффициент (w), характеризующий пропускную способность канала и оценивающий степень влияния сигнала с этого входа на сигнал на выходе. В зависимости от конкретной реализации, обрабатываемые нейроном сигналы могут быть аналоговыми или цифровыми (1 или 0). В теле нейрона происходит взвешенное суммирование входных возбуждений, и далее это значение является аргументом активационной функции нейрона, один из возможных вариантов которой представлен на Рис.  4.

Рис.  4 Искусственный нейрон

Будучи соединенными определенным образом, нейроны образуют нейронную сеть. Работа сети разделяется на обучение и адаптацию. Под обучением понимается процесс адаптации сети к предъявляемым эталонным образцам путем модификации (в соответствии с тем или иным алгоритмом) весовых коэффициентов связей между нейронами. Заметим, что этот процесс является результатом алгоритма функционирования сети, а не предварительно заложенных в нее знаний человека, как это часто бывает в системах искусственного интеллекта.

Среди различных структур нейронных сетей (НС) одной из наиболее известных является многослойная структура, в которой каждый нейрон произвольного слоя связан со всеми аксонами нейронов предыдущего слоя или, в случае первого слоя, со всеми входами НС. Такие НС называются полносвязными. Когда в сети только один слой, алгоритм ее обучения с учителем довольно очевиден, так как правильные выходные состояния нейронов единственного слоя заведомо известны, и подстройка синаптических связей идет в направлении, минимизирующем ошибку на выходе сети.
По этому принципу строится, например, алгоритм обучения однослойного перцептрона. В многослойных же сетях оптимальные выходные значения нейронов всех слоев, кроме последнего, как правило, не известны, и двух или более слойный перцептрон уже невозможно обучить, руководствуясь только величинами ошибок на выходах НС. Один из вариантов решения этой проблемы – разработка наборов выходных сигналов, соответствующих входным, для каждого слоя НС, что, конечно, является очень трудоемкой операцией и не всегда осуществимо. Второй вариант – динамическая подстройка весовых коэффициентов синапсов, в ходе которой выбираются, как правило, наиболее слабые связи и изменяются на малую величину в ту или иную сторону, а сохраняются только те изменения, которые повлекли уменьшение ошибки на выходе всей сети. Очевидно, что данный метод "тыка", несмотря на свою кажущуюся простоту, требует громоздких рутинных вычислений. И, наконец, третий, более приемлемый вариант – распространение сигналов ошибки от выходов НС к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Этот алгоритм обучения НС получил название процедуры обратного распространения. Именно он будет рассмотрен в дальнейшем.

Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки НС является величина:

                                                                                                                      (1)

где  – реальное выходное состояние нейрона j выходного слоя N нейронной сети при подаче на ее входы p-го образа; djp – идеальное (желаемое) выходное состояние этого нейрона.

Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация ведется методом градиентного спуска, что означает подстройку весовых коэффициентов следующим образом:

                                                                                                                                           (2)

Здесь wij – весовой коэффициент синаптической связи, соединяющей i-ый нейрон слоя n-1 с j-ым нейроном слоя n, h – коэффициент скорости обучения, 0<h<1.



Как показано в [2],

                                                                                                                                (3)

Здесь под yj, как и раньше, подразумевается выход нейрона j, а под sj – взвешенная сумма его входных сигналов, то есть аргумент активационной функции. Так как множитель dyj/dsj является производной этой функции по ее аргументу, из этого следует, что производная активационной функция должна быть определена на всей оси абсцисс. В связи с этим функция единичного скачка и прочие активационные функции с неоднородностями не подходят для рассматриваемых НС. В них применяются такие гладкие функции, как гиперболический тангенс или классический сигмоид с экспонентой. В случае гиперболического тангенса

                                                                                                                                                        (4)

Третий множитель ¶sj/¶wij, очевидно, равен выходу нейрона предыдущего слоя yi(n-1).

Что касается первого множителя в (3), он легко раскладывается следующим образом[2]:

                                                                                (5)

Здесь суммирование по k выполняется среди нейронов слоя n+1.

Введя новую переменную

                                                                                                                                              (6)

мы получим рекурсивную формулу для расчетов величин dj(n) слоя n из величин dk(n+1) более старшего слоя n+1.

                                                                                                                 (7)

Для выходного же слоя

                                                                                                                               (8)

Теперь мы можем записать (2) в раскрытом виде:

                                                                                                                              (9)

Иногда для придания процессу коррекции весов некоторой инерционности, сглаживающей резкие скачки при перемещении по поверхности целевой функции, (9) дополняется значением изменения веса на предыдущей итерации



                                                              (10)

где m – коэффициент инерционности, t – номер текущей итерации.

Таким образом, полный алгоритм обучения НС с помощью процедуры обратного распространения строится так:

1. Подать на входы сети один из возможных образов и в режиме обычного функционирования НС, когда сигналы распространяются от входов к выходам, рассчитать значения последних. Напомним, что

                                                                                                                                    (11)

где M – число нейронов в слое n-1 с учетом нейрона с постоянным выходным состоянием +1, задающего смещение; yi(n-1)=xij(n) – i-ый вход нейрона j слоя n.

yj(n) = f(sj(n)), где f() – сигмоид                                                                                                                          (12)

yq(0)=Iq,                                                                                                                                                                   (13)

где Iq – q-ая компонента вектора входного образа.

2. Рассчитать d(N) для выходного слоя по формуле (8).

Рассчитать по формуле (9) или (10) изменения весов Dw(N) слоя N.

3. Рассчитать по формулам (7) и (9) (или (7) и (10)) соответственно d(n) и Dw(n) для всех остальных слоев, n=N-1,...1.

4. Скорректировать все веса в НС

                                                                                                              (14)

5. Если ошибка сети существенна, перейти на шаг 1. В противном случае – конец.

Рис.  5. Диаграмма сигналов в сети при обучении по алгоритму обратного распространения

Сети на шаге 1 попеременно в случайном порядке предъявляются все тренировочные образы, чтобы сеть, образно говоря, не забывала одни по мере запоминания других. Алгоритм иллюстрируется Рис.  5.

Из выражения (9) следует, что когда выходное значение yi(n-1) стремится к нулю, эффективность обучения заметно снижается. При двоичных входных векторах в среднем половина весовых коэффициентов не будет коррек­тироваться[3], поэтому область возможных значений выходов нейронов [0,1] желательно сдвинуть в пределы [-0.5,+0.5], что достигается простыми модификациями логистических функций.


Например, сигмоид с экспонентой преобразуется к виду

                                                          (15)

Теперь коснемся вопроса емкости НС, то есть числа образов, предъявляемых на ее входы, которые она способна научиться распознавать. Для сетей с числом слоев больше двух, он остается открытым. Как показано в [4], для НС с двумя слоями, то есть выходным и одним скрытым слоем, детерминистская емкость сети Cd оценивается так:

Nw/Ny<Cd<Nw/Ny×log(Nw/Ny)                                                                                                                             (16)

где Nw – число подстраиваемых весов, Ny – число нейронов в выходном слое.

Следует отметить, что данное выражение получено с учетом некоторых ограничений. Во-первых, число входов Nx и нейронов в скрытом слое Nh должно удовлетворять неравенству Nx+Nh>Ny. Во-вторых, Nw/Ny>1000. Однако вышеприведенная оценка выполнялась для сетей с активационными функциями нейронов в виде порога, а емкость сетей с гладкими активационными функциями, например – (15), обычно больше. Кроме того, фигурирующее в названии емкости прилагательное "детерминистский" означает, что полученная оценка емкости подходит абсолютно для всех возможных входных образов, которые могут быть представлены Nx входами. В действительности распределение входных образов, как правило, обладает некоторой регулярностью, что позволяет НС проводить обобщение и, таким образом, увеличивать реальную емкость. Так как распределение образов, в общем случае, заранее не известно, мы можем говорить о такой емкости только предположительно, но обычно она раза в два превышает емкость детерминистскую.

В продолжение разговора о емкости НС логично затронуть вопрос о требуемой мощности выходного слоя сети, выполняющего окончательную классификацию образов. Дело в том, что для разделения множества входных образов, например, по двум классам достаточно всего одного выхода. При этом каждый логический уровень – "1" и "0" – будет обозначать отдельный класс.


На двух выходах можно закодировать уже 4 класса и так далее. Однако результаты работы сети, организованной таким образом, можно сказать – "под завязку", – не очень надежны. Для повышения достоверности классификации желательно ввести избыточность путем выделения каждому классу одного нейрона в выходном слое или, что еще лучше, нескольких, каждый из которых обучается определять принадлежность образа к классу со своей степенью достоверности, например: высокой, средней и низкой. Такие НС позволяют проводить классификацию входных образов, объединенных в нечеткие (размытые или пересекающиеся) множества. Это свойство приближает подобные НС к условиям реальной жизни.

Рассматриваемая НС имеет несколько "узких мест". Во-первых, в процессе обучения может возникнуть ситуация, когда большие положительные или отрицательные значения весовых коэффициентов сместят рабочую точку на сигмоидах многих нейронов в область насыщения. Малые величины производной от логистической функции приведут в соответствие с (7) и (8) к остановке обучения, что парализует НС. Во-вторых, применение метода градиентного спуска не гарантирует, что будет найден глобальный, а не локальный минимум целевой функции. Эта проблема связана еще с одной, а именно – с выбором величины скорости обучения. Доказательство сходимости обучения в процессе обратного распространения основано на производных, то есть приращения весов и, следовательно, скорость обучения должны быть бесконечно малыми, однако в этом случае обучение будет происходить неприемлемо медленно. С другой стороны, слишком большие коррекции весов могут привести к постоянной неустойчивости процесса обучения. Поэтому в качестве h обычно выбирается число меньше 1, но не очень маленькое, например, 0.1, и оно, вообще говоря, может постепенно уменьшаться в процессе обучения. Кроме того, для исключения случайных попаданий в локальные минимумы иногда, после того как значения весовых коэффициентов застабилизируются, h кратковременно сильно увеличивают, чтобы начать градиентный спуск из новой точки.Если повторение этой процедуры несколько раз приведет алгоритм в одно и то же состояние НС, можно более или менее уверенно сказать, что найден глобальный максимум, а не какой-то другой.

Существует и иной метод исключения локальных минимумов, а заодно и паралича НС, заключающийся в применении стохастических НС, но о них лучше поговорить отдельно.

Неформальные процедуры

Говоря о неформальных процедурах мы обычно хорошо понимаем, что имеется в виду, и без затруднений можем привести примеры таких процедур, связанных с пониманием текстов естественного языка, переводом с одного естественного языка на другой, информационным поиском по смыслу и т. д.

Трудности возникают при попытке точного определения подобных процедур. Так, если рассматривать неформальные процедуры всего лишь как абстрактные функции, которые для каждого значения аргумента "выдают" некоторое значение, то категория неформальности вообще исчезает из рассмотрения.

Неформальная процедура — это особый способ представления функций. Чтобы в какой-то степени приблизиться к этому "человеческому" способу представления функций, рассмотрим прежде всего традиционные алгоритмические модели и попытаемся понять, в чем состоит основная трудность их применения для имитации неформальных процедур.

Нейронные сети Хопфилда и Хэмминга

Среди различных конфигураций искуственных нейронных сетей (НС) встречаются такие, при классификации которых по принципу обучения, строго говоря, не подходят ни обучение с учителем, ни обучение без учителя. В таких сетях весовые коэффициенты синапсов рассчитываются только однажды перед началом функционирования сети на основе информации об обрабатываемых данных, и все обучение сети сводится именно к этому расчету. С одной стороны, предъявление априорной информации можно расценивать, как помощь учителя, но с другой – сеть фактически просто запоминает образцы до того, как на ее вход поступают реальные данные, и не может изменять свое поведение, поэтому говорить о звене обратной связи с "миром" (учителем) не приходится. Из сетей с подобной логикой работы наиболее известны сеть Хопфилда и сеть Хэмминга, которые обычно используются для организации ассоциативной памяти. Далее речь пойдет именно о них.

Структурная схема сети Хопфилда приведена на Рис.  6. Она состоит из единственного слоя нейронов, число которых является одновременно числом входов и выходов сети. Каждый нейрон связан синапсами со всеми остальными нейронами, а также имеет один входной синапс, через который осуществляется ввод сигнала. Выходные сигналы, как обычно, образуются на аксонах.

Рис.  6. Структурная схема сети Хопфилда.

Задача, решаемая данной сетью в качестве ассоциативной памяти, как правило, формулируется следующим образом. Известен некоторый набор двоичных сигналов (изображений, звуковых оцифровок, прочих данных, описывающих некие объекты или характеристики процессов), которые считаются образцовыми. Сеть должна уметь из произвольного неидеального сигнала, поданного на ее вход, выделить ("вспомнить" по частичной информации) соответствующий образец (если такой есть) или "дать заключение" о том, что входные данные не соответствуют ни одному из образцов. В общем случае, любой сигнал может быть описан вектором X = { xi: i=0...n-1}, n – число нейронов в сети и размерность входных и выходных векторов.
Каждый элемент xi равен либо +1, либо -1. Обозначим вектор, описывающий k-ый образец, через Xk, а его компоненты, соответственно, – xik, k=0...m-1, m – число образцов. Когда сеть распознáет (или "вспомнит") какой-либо образец на основе предъявленных ей данных, ее выходы будут содержать именно его, то есть Y = Xk, где Y – вектор выходных значений сети: Y = { yi: i=0,...n-1}. В противном случае, выходной вектор не совпадет ни с одним образцовым.

Если, например, сигналы представляют собой некие изображения, то, отобразив в графи­ческом виде данные с выхода сети, можно будет увидеть картинку, полностью совпадающую с одной из образцовых (в случае успеха) или же "вольную импровизацию" сети (в случае неудачи).

На стадии инициализации сети весовые коэффициенты синапсов устанавливаются следующим образом:

                                                                                                                                   (1)

Здесь i и j – индексы, соответственно, предсинаптического и постсинаптического нейронов; xik, xjk – i-ый и j-ый элементы вектора k-ого образца.

Алгоритм функционирования сети следующий (p – номер итерации):

1. На входы сети подается неизвестный сигнал. Фактически его ввод осуществляется непо­сред­ственной установкой значений аксонов:

yi(0) = xi , i = 0...n-1,                                                                                                                                           (2)

поэтому обозначение на схеме сети входных синапсов в явном виде носит чисто условный характер. Ноль в скобке справа от yi означает нулевую итерацию в цикле работы сети.

2. Рассчитывается новое состояние нейронов

, j=0...n-1                                                                                                             (3)

и новые значения аксонов

                                                                                                                            (4)

Рис.  7. Активационные функции.

где f – активационная функция в виде скачка, приве­денная на Рис.  7а.

3. Проверка, изменились ли выходные значения аксонов за последнюю итерацию. Если да – переход к пункту 2, иначе (если выходы застабилизировались) – конец. При этом выходной вектор представляет собой образец, наилучшим образом сочетающийся с входными данными.

Как говорилось выше, иногда сеть не может провести распознавание и выдает на выходе несуществующий образ. Это связано с проблемой ограниченности возможностей сети. Для сети Хопфилда число запоминаемых образов m не должно превышать величины, примерно равной 0.15•n. Кроме того, если два образа А и Б сильно похожи, они, возможно, будут вызывать у сети перекрестные ассоциации, то есть предъявление на входы сети вектора А приведет к появлению на ее выходах вектора Б и наоборот.

Рис.  8. Структурная схема сети Хэмминга.



Когда нет необходимости, чтобы сеть в явном виде выдавала образец, то есть достаточно, скажем, получать номер образца, ассоциативную память успешно реализует сеть Хэмминга. Данная сеть характеризуется, по сравнению с сетью Хопфилда, меньшими затратами на память и объемом вычислений, что становится очевидным из ее структуры (Рис.  8).

Сеть состоит из двух слоев. Первый и второй слои имеют по m нейронов, где m – число образцов. Нейроны первого слоя имеют по n синапсов, соединенных со входами сети (образующими фиктивный нулевой слой). Нейроны второго слоя связаны между собой ингибиторными (отрицательными обратными) синаптическими связями. Единственный синапс с положительной обратной связью для каждого нейрона соединен с его же аксоном.

Идея работы сети состоит в нахождении расстояния Хэмминга от тестируемого образа до всех образцов. Расстоянием Хэмминга называется число отличающихся битов в двух бинарных векторах. Сеть должна выбрать образец с минимальным расстоянием Хэмминга до неизвестного входного сигнала, в результате чего будет активизирован только один выход сети, соответствующий этому образцу.

На стадии инициализации весовым коэффициентам первого слоя и порогу активационной функции присваиваются следующие значения:



, i=0...n-1, k=0...m-1                                                                                                                      (5)

Tk = n / 2, k = 0...m-1                                                                                                                                           (6)

Здесь xik – i-ый элемент k-ого образца.

Весовые коэффициенты тормозящих синапсов во втором слое берут равными некоторой величине 0 < e < 1/m. Синапс нейрона, связанный с его же аксоном имеет вес +1.

Алгоритм функционирования сети Хэмминга следующий:

1. На входы сети подается неизвестный вектор X = {xi:i=0...n-1}, исходя из которого рассчитываются состояния нейронов первого слоя (верхний индекс в скобках указывает номер слоя):

, j=0...m-1                                                                                                        (7)

После этого полученными значениями инициализируются значения аксонов второго слоя:

yj(2) = yj(1), j = 0...m-1                                                                                                                                           (8)

2. Вычислить новые состояния нейронов второго слоя:

                                                                (9)

и значения их аксонов:

                                                                                         (10)

Активационная функция f имеет вид порога (рис. 2б), причем величина F должна быть достаточно большой, чтобы любые возможные значения аргумента не приводили к насыщению.

3. Проверить, изменились ли выходы нейронов второго слоя за последнюю итерацию. Если да – перейди к шагу 2. Иначе – конец.

Из оценки алгоритма видно, что роль первого слоя весьма условна: воспользовавшись один раз на шаге 1 значениями его весовых коэффициентов, сеть больше не обращается к нему, поэтому первый слой может быть вообще исключен из сети (заменен на матрицу весовых коэффициентов).

Нейронные сети: обучение без учителя

Рассмотренный в предыдущей главе алгоритм обучения нейронной сети с помощью процедуры обратного распространения подразумевает наличие некоего внешнего звена, предоставляющего сети кроме входных так же и целевые выходные образы. Алгоритмы, пользующиеся подобной концепцией, называются алгоритмами обучения с учителем. Для их успешного функционирования необходимо наличие экспертов, создающих на предварительном этапе для каждого входного образа эталонный выходной. Так как создание искусственного интеллекта движется по пути копирования природных прообразов, ученые не прекращают спор на тему, можно ли считать алгоритмы обучения с учителем натуральными или же они полностью искусственны. Например, обучение человеческого мозга, на первый взгляд, происходит без учителя: на зрительные, слуховые, тактильные и прочие рецепторы поступает информация извне, и внутри нервной системы происходит некая самоорганизация. Однако, нельзя отрицать и того, что в жизни человека не мало учителей – и в буквальном, и в переносном смысле, – которые координируют внешние воздействия. Вместе в тем, чем бы ни закончился спор приверженцев этих двух концепций обучения, они обе имеют право на существование.

Главная черта, делающая обучение без учителя привлекательным, – это его "самостоятельность". Процесс обучения, как и в случае обучения с учителем, заключается в подстраивании весов синапсов. Некоторые алгоритмы, правда, изменяют и структуру сети, то есть количество нейронов и их взаимосвязи, но такие преобразования правильнее назвать более широким термином – самоорганизацией, и в рамках данной главы они рассматриваться не будут. Очевидно, что подстройка синапсов может проводиться только на основании информации, доступной в нейроне, то есть его состояния и уже имеющихся весовых коэффициентов. Исходя из этого соображения и, что более важно, по аналогии с известными принципами самоорганизации нервных клеток, построены алгоритмы обучения Хебба.

Сигнальный метод обучения Хебба заключается в изменении весов по следующему правилу:

                                                                                                         (1)

где yi(n-1) – выходное значение нейрона i слоя (n-1), yj(n) – выходное значение нейрона j слоя n; wij(t) и wij(t-1) – весовой коэффициент синапса, соединяющего эти нейроны, на итерациях t и t?1 соответственно; a – коэффициент скорости обучения. Здесь и далее, для общности, под n подразу­мевается произвольный слой сети. При обучении по данному методу усиливаются связи между возбужденными нейронами.

Существует также и дифференциальный метод обучения Хебба.

                                (2)

Здесь yi(n-1)(t) и yi(n-1)(t-1) – выходное значение нейрона i слоя n-1 соответственно на итерациях t и t-1; yj(n)(t) и yj(n)(t-1) – то же самое для нейрона j слоя n. Как видно из формулы (2), сильнее всего обучаются синапсы, соединяющие те нейроны, выходы которых наиболее динамично изменились в сторону увеличения.

Полный алгоритм обучения с применением вышеприведенных формул будет выглядеть так:

1. На стадии инициализации всем весовым коэффициентам присваиваются небольшие слу­чай­ные значения.

2. На входы сети подается входной образ, и сигналы возбуждения распространяются по всем слоям согласно принципам классических прямопоточных (feedforward) сетей[1], то есть для каждого нейрона рассчитывается взвешенная сумма его входов, к которой затем применяется активационная (передаточная) функция нейрона, в результате чего получается его выходное значение yi(n), i=0...Mi-1, где Mi – число нейронов в слое i; n=0...N-1, а N – число слоев в сети.

3. На основании полученных выходных значений нейронов по формуле (1) или (2) произво­дится изменение весовых коэффициентов.

4. Цикл с шага 2, пока выходные значения сети не застабилизируются с заданной точнос­тью. Применение этого нового способа определения завершения обучения, отличного от исполь­зо­вавшегося для сети обратного распространения, обусловлено тем, что подстраиваемые зна­че­ния синапсов фактически не ограничены.



На втором шаге цикла попеременно предъявляются все образы из входного набора.

Следует отметить, что вид откликов на каждый класс входных образов не известен заранее и будет представлять собой произвольное сочетание состояний нейронов выходного слоя, обусловленное случайным распределением весов на стадии инициализации. Вместе с тем, сеть способна обобщать схожие образы, относя их к одному классу. Тестирование обученной сети позволяет определить топологию классов в выходном слое. Для приведения откликов обученной сети к удобному представлению можно дополнить сеть одним слоем, который, например, по алгоритму обучения однослойного перцептрона необходимо заставить отображать выходные реак­ции сети в требуемые образы.

Другой алгоритм обучения без учителя – алгоритм Кохонена – предусматривает подстройку синапсов на основании их значений от предыдущей итерации.

                                                                                        (3)

Из вышеприведенной формулы видно, что обучение сводится к минимизации разницы между входными сигналами нейрона, поступающими с выходов нейронов предыдущего слоя yi(n?1), и весовыми коэффициентами его синапсов.

Полный алгоритм обучения имеет примерно такую же структуру, как в методах Хебба, но на шаге 3 из всего слоя выбирается нейрон, значения синапсов которого максимально походят на входной образ, и подстройка весов по формуле (3) проводится только для него. Эта, так называемая, аккре­ди­тация может сопровождаться затормаживанием всех остальных нейронов слоя и введе­нием выбранного нейрона в насыщение. Выбор такого нейрона может осуществляться, например, рас­че­том скалярного произведения вектора весовых коэффициентов с вектором входных значе­ний. Максимальное произведение дает выигравший нейрон.

Другой вариант – расчет расстояния между этими векторами в p-мерном пространстве, где p – размер векторов.

,                                                                                                                           (4)



где j – индекс нейрона в слое n, i – индекс суммирования по нейронам слоя (n-1), wij – вес синапса, соединяющего нейроны; выходы нейронов слоя (n-1) являются входными значениями для слоя n. Корень в формуле (4) брать не обязательно, так как важна лишь относительная оценка различных Dj.

В данном случае, "побеждает" нейрон с наименьшим расстоянием. Иногда слишком часто получающие аккредитацию нейроны принудительно исключаются из рассмотрения, чтобы "урав­нять права" всех нейронов слоя. Простейший вариант такого алгоритма заключается в торможении только что выигравшего нейрона.

При использовании обучения по алгоритму Кохонена существует практика нормализации входных образов, а так же – на стадии инициализации – и нормализации начальных значений весовых коэффициентов.

,                                                                                                                                            (5)

где xi – i-ая компонента вектора входного образа или вектора весовых коэффициентов, а n – его размерность. Это позволяет сократить длительность процесса обучения.

Инициализация весовых коэффициентов случайными значениями может привести к тому, что различные классы, которым соответствуют плотно распределенные входные образы, сольются или, наоборот, раздробятся на дополнительные подклассы в случае близких образов одного и того же класса. Для избежания такой ситуации используется метод выпуклой комбинации[3]. Суть его сводится к тому, что входные нормализованные образы подвергаются преобразованию:

,                                                                                                               (6)

где xi – i-ая компонента входного образа, n – общее число его компонент, a(t) – коэф­фи­ци­ент, изменяющийся в процессе обучения от нуля до единицы, в результате чего вначале на входы сети подаются практически одинаковые образы, а с течением времени они все больше сходятся к исходным. Весовые коэффициенты устанавливаются на шаге инициализации равными величине



,                                                                                                                                                          (7)

где n – размерность вектора весов для нейронов инициализируемого слоя.

На основе рассмотренного выше метода строятся нейронные сети особого типа – так назы­ва­емые самоорганизующиеся структуры – self-organizing feature maps (этот устоявшийся перевод с английского, на мой взгляд, не очень удачен, так как, речь идет не об изменении структуры сети, а только о подстройке синапсов). Для них после выбора из слоя n нейрона j с минимальным расстоянием Dj (4) обучается по формуле (3) не только этот нейрон, но и его соседи, расположенные в окрестности R. Величина R на первых итерациях очень большая, так что обучаются все нейроны, но с течением времени она уменьшается до нуля. Таким образом, чем ближе конец обучения, тем точнее определяется группа нейронов, отвечающих каждому классу образов.

ОБЛАСТЬ ДЕЙСТВИЯ ПЕРЕМЕННЫХ

Областью действия переменной является утверждение. В преде­лах утверждения одно и то же имя принадлежит одной и той же пе­ременной. Два утверждения могут использовать одно имя перемен­ной совершенно различным образом. Правило определения области действия переменной справедливо также в случае рекурсии и в том случае, когда несколько утверждений имеют одну и ту же головную цель. Этот вопрос будет рассмотрен в далее.

Единственным исключением из правила определения области действия переменных является анонимная переменная, например, «_» в цели любит(Х,_). Каждая анонимная переменная есть отдель­ная сущность. Она применяется тогда, когда конкретное значение переменной несущественно для данного утверждения. Таким обра­зом, каждая анонимная переменная четко отличается от всех других анонимных переменных в утверждении.

Переменные, отличные от анонимных, называются именованны­ми, а неконкретизированные (переменные, которым не было присво­ено значение) называются свободными.

Общая схема построения алгоритмов метода группового учета аргументов (МГУА).

Рис.  9. Селекция самого черного тюльпана при расширяющемся опытном поле (эквивалент полного перебора), и при постоянном размере поля (эквивалент селекции при сохранении свободы выбора решений F = const).

Заимствование алгоритмов переработки информации у природы является одной из основных идей кибернетики. "Гипотеза селекции" утверждает, что алгоритм массовой селекции растений или животных является оптимальным алгоритмом переработки информации в сложных задачах. При массовой селекции высевается некоторое количество семян. В результате опыления образуются сложные наследственные комбинации. Селекционеры выбирают некоторую часть растений, у которых интересующее их свойство выражено больше всего (эвристический критерий). Семена этих растений собирают и снова высевают для образования новых, еще более сложных комбинаций. Через несколько поколений селекция останавливается и ее результат является оптимальным. Если чрезмерно продолжать селекцию, то наступит «инцухт» — вырождение растений. Существует оптимальное число поколений и оптимальное количество семян, отбираемых в каждом из них.

Алгоритмы МГУА воспроизводят схему массовой селекции [5], показанной на Рис.  9. В них есть генераторы усложняющихся из ряда в ряд комбинаций и пороговые самоотборы лучших из них. Так называемое «полное» описание объекта

j = f(x1,x2,x3,¼,xm),

где f — некоторая элементарная функция, например степенной полином, заменяется несколькими рядами "частных" описаний:

1-ряд селекции: y1= f(x1x2), y2= f(x1x3),..., ys= f(xm-1xm),

2-ряд селекции: z1= f(y1y2), z2= f(y1y2),..., zp= f(ys-1ys), где s=c2, p=cs2 и т.д.

Входные аргументы и промежуточные переменные сопрягаются попарно, и сложность комбинаций на каждом ряду обработки информации возрастает (как при массовой селекции), пока не будет получена единственная модель оптимальной сложности.

Каждое частное описание является функцией только двух аргументов. Поэтому его коэффициенты легко определить по данным обучающей последовательности при малом числе узлов интерполяции [4].
Исключая промежуточные переменные (если это удается), можно получить "аналог" полного описания. Математика не запрещает обе эти операции. Например, по десяти узлам интерполяции можно получить в результате оценки коэффициентов полинома сотой степени и т. д.

Из ряда в ряд селекции пропускается только некоторое количество самых регулярных переменных. Степень регулярности оценивается по величине среднеквадратичной ошибки (средней для всех выбираемых в каждом поколении переменных или для одной самой точной переменой) на отдельной проверочной последовательности данных. Иногда в качестве показателя регулярности используется коэффициент корреляции.

Ряды селекции наращиваются до тех пор, пока регулярность повышается. Как только достигнут минимум ошибки, селекцию, во избежание "инцухта", следует остановить. Практически рекомендуется остановить селекцию даже несколько раньше достижения полного минимума, как только ошибка начинает падать слишком медленно. Это приводит к более простым и более достоверным уравнениям.

Обучение и самообучение. Адаптация и обучение

Все картинки, представленные на Рис.  1, характеризуют задачу обучения. В каждой из этих задач задается несколько примеров (обучающая последовательность) правильно решенных задач. Если бы удалось подметить некое всеобщее свойство, не зависящее ни от природы образов, на от их изображений, а определяющее лишь их способность к разделимости, то наряду с обычной задачей обучения распознаванию, с использованием информации о принадлежности каждого объекта из обучающей последовательности тому или иному образу можно было бы поставить иную классификационную задачу — так называемую задачу обучения без учителя. Задачу такого рода на описательном уровне можно сформулировать следующим образом: системе одновременно или последовательно предъявляются объекты без каких-либо указаний об их принадлежности к образам. Входное устройство системы отображает множество объектов на множество изображений и, используя некоторое заложенное в нее заранее свойство разделимости образов, производит самостоятельную классификацию этих объектов. После такого процесса самообучения система должна приобрести способность к распознаванию не только уже знакомых объектов (объектов из обучающей последовательности), но и тех, которые ранее не предъявлялись. Процессом самообучения некоторой системы называется такой процесс, в результате которого эта система без подсказки учителя приобретает способность к выработке одинаковых реакций на изображения объектов одного и того же образа и различных реакций на изображения различных образов. Роль учителя при этом состоит лишь в подсказке системе некоторого объективного свойства, одинакового для всех образов и определяющего способность к разделению множества объектов на образы.

Оказывается, таким объективным свойством является свойство компактности образов. Взаимное расположение точек в выбранном пространстве уже содержит информацию о том, как следует разделить множество точек. Эта информация и определяет то свойство разделимости образов, которое оказывается достаточным для самообучения системы распознаванию образов.

Большинство известных алгоритмов самообучения способны выделять только абстрактные образы, т. е. компактные множества в заданных пространствах. Различие между ними состоит, по-видимому, в формализации понятия компактности. Однако это не снижает, а иногда и повышает ценность алгоритмов самообучения, так как часто сами образы заранее никем не определены, а задача состоит в том, чтобы определить, какие подмножества изображений в заданном пространстве представляют собой образы. Хорошим примером такой постановки задачи являются социологические исследования, когда по набору вопросов выделяются группы людей. В таком понимании задачи алгоритмы самообучения генерируют заранее не известную информацию о существовании в заданном пространстве образов, о которых ранее никто не имел никакого представления.

Кроме того, результат самообучения характеризует пригодность выбранного пространства для конкретной задачи обучения распознаванию. Если абстрактные образы, выделяемые в процессе самообучения, совпадают с реальными, то пространство выбрано удачно. Чем сильнее абстрактные образы отличаются от реальных, тем "неудобнее" выбранное пространство для конкретной задачи.

Обучением обычно называют процесс выработки в некоторой системе той или иной реакции на группы внешних идентичных сигналов путем многократного воздействия на систему внешней корректировки. Такую внешнюю корректировку в обучении принято называть "поощрениями" и "наказаниями". Механизм генерации этой корректировки практически полностью определяет алгоритм обучения. Самообучение отличается от обучения тем, что здесь дополнительная информация о верности реакции системе не сообщается.

Адаптация — это процесс изменения параметров и структуры системы, а возможно, и управляющих воздействий на основе текущей информации с целью достижения определенного состояния системы при начальной неопределенности и изменяющихся условиях работы.

Обучение — это процесс, в результате которого система постепенно приобретает способность отвечать нужными реакциями на определенные совокупности внешних воздействий, а адаптация — это подстройка параметров и структуры системы с целью достижения требуемого качества управления в условиях непрерывных изменений внешних условий.

Отождествимы ?

джек(Х)

джек (личность)

джек(Х,Х)

джек(Х.Х)

джек( . )

f(Y,Z)

Х

джек (человек)

джек (человек)

джек(23,23)

джек (12,23)

джек(12,23)

Х

Z

да: Х=человек

нет

да: Х=23

нет

да

да: X=f(Y,Z)

да: X=Z

Заметим, что Пролог находит наиболее общий унификатор тер­мов. В последнем примере (рис.2.1) существует бесконечное число унификаторов:

X-1, Z-2; X-2, Z-2; ....

но Пролог находит наиболее общий: Х=Z.

Следует сказать, что в большинстве реализации Пролога для по­вышения эффективности его работы допускается существование циклических унификаторов. Например, попытка отождествить тер­мы f(X) и Х приведет к циклическому унификатору X=f(X), кото­рый определяет бесконечный терм f(f(f(f(f(...))))). В программе это иногда вызывает бесконечный цикл.

Возможность отождествления двух термов проверяется с по­мощью оператора =.

Ответом на запрос

?- 3+2=5.

будет

нет

так как термы не отождествимы (оператор не вычисляет значения своих аргументов), но попытка доказать

?-строка(поз(Х)) -строка(поз(23)).

закончится успехом при

Х=23.

Унификация часто используется для доступа к подкомпонентам термов. Так, в вышеприведенном примере Х конкретизируется пер­вой компонентой терма поз(23), который в свою очередь является компонентой терма строка.

Бывают случаи, когда надо проверить, идентичны ли два терма. Выполнение оператора = = заканчивается успехом, если его аргумен­ты - идентичные термы. Следовательно, запрос

?-строка(поз(Х)) --строка (поз (23)).

дает ответ

нет

поскольку подтерм Х в левой части (X - свободная переменная) не идентичен подтерму 23 в правой части, Однако запрос

?- строка (поз (23)) --строка (поз (23)).

дает ответ

да

Отрицания операторов = и - = записываются как \= и \= = соот­ветственно.

Перцептроны

Пока о проблеме обучения распознаванию образов удавалось говорить в общих чертах, не выделяя конкретные методы или алгоритмы, не возникало и трудностей, появляющихся всяких раз, когда приходится в огромном множестве конкретных примеров, характеризующиеся общими подходами к решению проблемы ОРО. Коварство самой проблемы состоит в том, что на первый взгляд все методы и алгоритмы кажутся совершенно различными и, что самое неприятное, часто никакой из них не годится для решения той задачи, которую крайне необходимо срочно решить. И тогда появляется желание выдумать новый алгоритм, который, может быть, достигнет цели. Очевидно, именно это привело к возникновению огромного множества алгоритмов, в котором не так-то легко разобраться.

Одним из методов решения задач обучения распознаванию образов основан на моделировании гипотетического механизма человеческого мозга. Структура модели заранее постулируется. При таком подходе уровень биологических знаний или гипотез о биологических механизмах является исходной предпосылкой, на которой базируются модели этих механизмов. Примером такого направления в теории и практике проблемы ОРО является класс устройств, называемых перцептронами. Нужно отметить, что перцептроны на заре своего возникновения рассматривались только как эвристические модели механизма мозга. Впоследствии они стали основополагающей схемой в построении кусочно-линейных моделей, обучающихся распознаванию образов.

Рис.  3

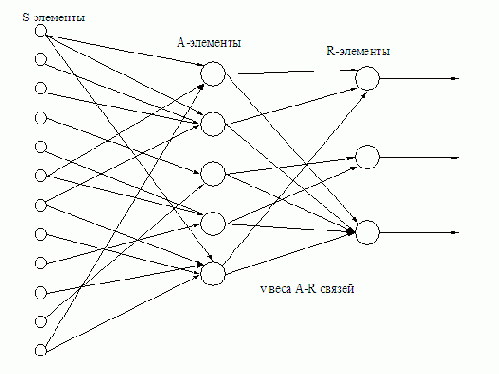
В наиболее простом виде перцептрон (Рис.  3) состоит из совокупности чувствительных (сенсорных) элементов (S-элементов), на которые поступают входные сигналы. S-элементы случайным образом связаны с совокупностью ассоциативных элементов (А-элементов), выход которых отличается от нуля только тогда, когда возбуждено достаточно большое число S-элементов, воздействующих на один А-элемент. А-элементы соединены с реагирующими элементами (R-элементами) связями, коэффициенты усиления (v) которых переменны и изменяются в процессе обучения. Взвешенные комбинации выходов R-элементов составляют реакцию системы, которая указывает на принадлежность распознаваемого объекта определенному образу.
Если распознаются только два образа, то в перцептроне устанавливается только один R-элемент, который обладает двумя реакциями — положительной и отрицательной. Если образов больше двух, то для каждого образа устанавливают свой R-элемент, а выход каждого такого элемента представляет линейную комбинацию выходов A-элементов:

,                                                                                                       (ф.  1)

где Rj — реакция j-го R-элемента; xi — реакция i-го A-элемента; vij — вес связи от i-го A-элемента к j-му R элементу; Qj — порог j-го R-элемента.

Аналогично записывается уравнение i-го A-элемента:

,                                                                                                              (ф.  2)

Здесь сигнал yk может быть непрерывным, но чаще всего он принимает только два значения: 0 или 1. Сигналы от S-элементов подаются на входы А-элементов с постоянными весами равными единице, но каждый А-элемент связан только с группой случайно выбранных S-элементов. Предположим, что требуется обучить перцептрон различать два образа V1 и V2. Будем считать, что в перцептроне существует два R-элемента, один из которых предназначен образу V1, а другой — образу V2. Перцептрон будет обучен правильно, если выход R1 превышает R2, когда распознаваемый объект принадлежит образу V1, и наоборот. Разделение объектов на два образа можно провести и с помощью только одного R-элемента. Тогда объекту образа V1 должна соответствовать положительная реакция R-элемента, а объектам образа V2 — отрицательная.

Перцептрон обучается путем предъявления обучающей последовательности изображений объектов, принадлежащих образам V1 и V2. В процессе обучения изменяются веса vi А-элементов. В частности, если применяется система подкрепления с коррекцией ошибок, прежде всего учитывается правильность решения, принимаемого перцептроном. Если решение правильно, то веса связей всех сработавших А-элементов, ведущих к R-элементу, выдавшему правильное решение, увеличиваются, а веса несработавших А-элементов остаются неизменными.


Можно оставлять неизменными веса сработавших А-элементов, но уменьшать веса несработавших. В некоторых случаях веса сработавших связей увеличивают, а несработавших — уменьшают. После процесса обучения перцептрон сам, без учителя, начинает классифицировать новые объекты.

Если перцептрон действует по описанной схеме и в нем допускаются лишь связи, идущие от бинарных S-элементов к A-элементам и от A-элементов к единственному R-элементу, то такой перцептрон принято называть элементарным a-перцептроном. Обычно классификация C(W) задается учителем. Перцептрон должен выработать в процессе обучения классификацию, задуманную учителем.

О перцептронах было сформулировано и доказано несколько основополагающих теорем, две из которых, определяющие основные свойства перцептрона, приведены ниже.

Теорема 1. Класс элементарных a-перцептронов, для которых существует решение для любой задуманной классификации, не является пустым.

Эта теорема утверждает, что для любой классификации обучающей последовательности можно подобрать такой набор (из бесконечного набора) А-элементов, в котором будет осуществлено задуманное разделение обучающей последовательности при помощи линейного решающего правила ).

Теорема 2. Если для некоторой классификации C(W) решение существует, то в процессе обучения a-перцептрона с коррекцией ошибок, начинающегося с произвольного исходного состояния, это решение будет достигнуто в течение конечного промежутка времени.

Смысл этой теоремы состоит в том, что если относительно задуманной классификации можно найти набор А-элементов, в котором существует решение, то в рамках этого набора оно будет достигнуто в конечный промежуток времени.

Обычно обсуждают свойства бесконечного перцептрона, т. е. перцептрона с бесконечным числом А-элементов со всевозможными связями с S-элементами (полный набор A-элементов). В таких перцептронах решение всегда существует, а раз оно существует, то оно и достижимо в a-перцептронах с коррекцией ошибок.

Очень интересную область исследований представляют собой многослойные перцептроны и перцептроны с перекрестными связями, но теория этих систем практически еще не разработана.

ПЕРЕМЕННЫЕ

Понятие переменной в Прологе отличается от принятого во мно­гих языках программирования. Переменная не рассматривается как выделенный участок памяти. Она служит для обозначения объекта, на который нельзя сослаться по имени. Переменную можно считать локальным именем для некоторого объекта.

Синтаксис переменной довольно прост. Она должна начинаться с прописной буквы или символа подчеркивания и содержать только символы букв, цифр и подчеркивания.

Переменная, состоящая только из символа подчеркивания, назы­вается анонимной и используется в том случае, если имя переменной несущественно.

Понятие образа

Образ, класс — классификационная группировка в системе классификации, объединяющая (выделяющая) определенную группу объектов по некоторому признаку.

Образное восприятие мира — одно из загадочных свойств живого мозга, позволяющее разобраться в бесконечном потоке воспринимаемой информации и сохранять ориентацию в океане разрозненных данных о внешнем мире. Воспринимая внешний мир, мы всегда производим классификацию воспринимаемых ощущений, т. е. разбиваем их на группы похожих, но не тождественных явлений. Например, несмотря на существенное различие, к одной группе относятся все буквы А, написанные различными почерками, или все звуки, соответствующие одной и той же ноте, взятой в любой октаве и на любом инструменте, а оператор, управляющий техническим объектом, на целое множество состояний объекта реагирует одной и той же реакцией. Характерно, что для составления понятия о группе восприятий определенного класса достаточно ознакомиться с незначительным количеством ее представителей. Ребенку можно показать всего один раз какую-либо букву, чтобы он смог найти эту букву в тексте, написанном различными шрифтами, или узнать ее, даже если она написана в умышленно искаженном виде. Это свойство мозга позволяет сформулировать такое понятие, как образ.

Образы обладают характерным свойством, проявляющимся в том, что ознакомление с конечным числом явлений из одного и того же множества дает возможность узнавать сколь угодно большое число его представителей. Примерами образов могут быть: река, море, жидкость, музыка Чайковского, стихи Маяковского и т. д. В качестве образа можно рассматривать и некоторую совокупность состояний объекта управления, причем вся эта совокупность состояний характеризуется тем, что для достижения заданной цели требуется одинаковое воздействие на объект. Образы обладают характерными объективными свойствами в том смысле, что разные люди, обучающиеся на различном материале наблюдений, большей частью одинаково и независимо друг от друга классифицируют одни и те же объекты. Именно эта объективность образов позволяет людям всего мира понимать друг друга.

Способность восприятия внешнего мира в форме образов позволяет с определенной достоверностью узнавать бесконечное число объектов на основании ознакомления с конечным их числом, а объективный характер основного свойства образов позволяет моделировать процесс их распознавания. Будучи отражением объективной реальности, понятие образа столь же объективно, как и сама реальность, а поэтому это понятие может быть само по себе объектом специального исследования.

В литературе, посвященной проблеме обучения распознавания образов (ОРО), часто вместо понятия образа вводится понятие класса.

ПРЕДСТАВЛЕНИЕ БИНАРНЫХ ДЕРЕВЬЕВ

Бинарное дерево определяется рекурсивно как имеющее левое поддерево, корень и правое поддерево. Левое и правое поддеревья са­ми являются бинарными деревьями. На Рис.  14 показан пример би­нарного дерева.

Рис.  14. Бинарное дерево.

Такие деревья можно представить термами вида

бд(Лд, К, Пд),

где Лд - левое поддерево, К - корень, а Пд - правое поддерево. Дл» обозначения пустого бинарного дерева будем использовать атом nil. Бинарное дерево на рис.5.2.1 имеет левое поддерево

бд(бд(nil, d, nil), b, бд(nil, е, nil))

правое поддерево

бд(nil,с, nil)

и записывается целиком как

бд(бд(бд(nil,d, nil), b, бд(nil,е, nil)), а, бд(nil, с, nil)).

ПРЕДСТАВЛЕНИЕ МНОЖЕСТВ С ПОМОЩЬЮ БИНАРНЫХ ДЕРЕВЬЕВ

Описание множеств в виде списков позволяет использовать для множеств целевое утверждение принадлежит, определенное ранее для списков.

Однако для множеств, состоящих из большого числа элементов, списковые целевые утверждения становятся неэффективными. Рас­смотрим, например, как целевое утверждение принадлежит (см. предыдущий разд.) позволяет моделировать принадлежность множеству. Пусть L - список, описывающий множество из первых 1024 нату­ральных чисел. Тогда при ответе на запрос

?- принадлежит(3000, b).

Прологу придется проверить все 1024 числа, прежде чем заключить, что такого числа нет:

нет

Представление множества бинарным деревом позволяет добиться лучшего результата. При этом бинарное дерево должно быть упоря­дочено таким образом, чтобы любой элемент в левом поддереве был меньше, чем значение корня, а любой элемент в правом поддереве — больше. Поскольку мы определили поддерево как бинарное дерево, такое упорядочение применяется по всем поддеревьям. На Рис.  15 приведен пример упорядоченного бинарного дерева.

Дерево на Рис.  14 является неупорядоченным.

Рис.  15. Упорядоченное бинарное дерево.

Обратите внимание, что упорядочение приводит не к единствен­ному варианту представления множества с помощью дерева. Напри­мер, на Рис.  16 изображено то же множество, что и на Рис.  15.

Будем называть линейным представление такого вида, как на Рис.  16, и сбалансированным - такое, как на Рис.  15.

Рис.  16. Линейное представление.

Моделирование принадлежности множеству. Имея множество, описанное бинарным деревом, мы можем моделировать принадлежность множеству с помощью целевого утверждения          принадлежит_дереву. При этом используется оператор @<, выражающий от­ношение «меньше, чем», и оператор @>, выражающий отношение «больше, чем».

/* Граничное условие: Х принадлежит

/* дереву, если Х является корнем.

принадлежит_дереву(Х, бд(Лд, Х, Пд)),

/* Рекурсивные условия

/* Х принадлежит дереву, если Х больше

/* значении корня и находится в правом

/* поддереве:

принадлсжит_дереву(Х, бд(Лд, У, Пд)) :- X@Y,

припадлежит_дереву(Х, Пд).

/* Х принадлежит дереву, если Х меньше

/* значения корня и находится в левом

/* поддереве:

принадлежит_дереву(Х, бд(Лд ,У ,Пд)) :-X@Y,

принадлежит_дереву(Х, Лд).

Если множество из первых 1024 чисел описать с помощью сба­лансированного бинарного дерева Т, то при ответе на запрос

?- принадлежит_дереву(3000, Т).

Пролог сравнит число 3000 не более чем с 11 элементами множества. прежде чем ответит:

нет

Конечно, если Т имеет линейное представление, то потребуется сравнение 3000 с 1024 элементами множества.

Построение бинарного дерева. Задача создания упорядоченного бинарного дерева при добавлении элемента Х к другому упорядочен­ному бинарному дереву формулируется следующим образом:

Граничное условие:

Добавление Х к nil дает бд(nil, Х, nil).

Рекурсивные условия:

При добавлении Х к бд(Лд, К, Пд) нужно рассмотреть два случая, чтобы быть уверенным, что результирующее дерево будет упорядо­ченным.

1. Х меньше,чем К. В этом случае нужно добавить Х к Лд, чтобы получить левое поддерево. Правое поддерево равно Пд, а значение корня результирующего дерева равно К.

2. Х больше, чем К. В таком случае нужно добавить Х к Пд, что­бы получить правое поддерево. Левое поддерево равно Лд, а значе­ние корня - К.

Такой формулировке задачи соответствует программа:

/* Граничное условие:

включ_бд(nil, Х, бд(nil, Х, nil)).

/* Рекурсивные условия:

/*(1)

включ_бд(бд(Лд, К, Пд), Х, бд(Лднов, К, Пд)) :-

Х@К,

включ_бд(Лд,Х,Лднов).

/*(2)

включ_бд(бд(Лд, К, Пд), Х, бд(Лд, К, Пднов)) :-

Х@К,

включ_бд(Пд, Х, Пднов).

На запрос

?- включ_бд(nil, d, Т1), включ_бд(Т1, а, Т2).

будут получены значения

Т1=бд(nil, d, nil)

Т2=бд(бд(nil, а, nil), d, nil)

Процедуру включ_бд() можно использовать для построения упо­рядоченного дерева из списка:

/* Граничное условие:

список_в_дерево([], nil).

/* Рекурсивное условие:

список_в_дерево([Н | Т], Бд) :-

список_в_дерево(Т, Бд2),

включ_бд(Н, Бд2, Бд).

Заметим, что включ_бд не обеспечивает построения сбалансиро­ванного дерева. Однако существуют алгоритмы, гарантирующие та­кое построение.

задача поиска пути в лабиринте

В качестве примера использования механизма возврата напишем процедуру для поиска пути в лабиринте. Лабиринт представлен фак­тами вида:

стена(I, J)                               для позиции в I-м ряду и J-й колонке, где есть стена

отсутств_стена(I, J)             для позиции в I-м ряду и J-й колонке, где нет стены

выход (I, J)                             для позиции в 1-м ряду и J-й колонке, являющейся выходом

Рассмотрим небольшой лабиринт:

Выход

Последний ряд лабиринта описывается фактами:

стена(4,1).

стена(4,3).

стена(4,4).

отсутств_стена(4,2).

Если задана исходная позиция, путь к выходу можно найти сле­дующим образом.

Граничное условие:

Если исходная позиция является выходом, то путь найден.

Рекурсивные условия:

Ищем путь из исходной позиции в северном направлении. Если пути нет, идем на юг. Если пути нет, идем на запад. Если нельзя, идем на восток. Если соседняя позиция на севере (юге, западе, восто­ке) является стеной, то нет смысла искать путь из начальной пози­ции к выходу. Чтобы не ходить кругами, будем вести список пози­ций, в которых мы побывали.

Изложенному способу решения задачи соответствует процедура путь: она ищет путь (второй аргумент) к выходу из некоторой пози­ции (первый аргумент). Третьим аргументом является список пози­ций, где мы побывали.

/* Терм a(I, J) представляет позицию в

/* I-м ряду и J-й колонке.

/* Нашли путь ?

путь(а(I, J),[а(I, J)], Были) :- выход(I, J).

/* Пытаемся идти на север

путь(а(I, J),[а(I, J) | Р], Были) :-

К is I-1,

можем_идти(a (K, J), Были),

путь(а(I, J) ,Р, [a(K, J) | Были]).

/* Пытаемся идти на юг

путь(а(I, J),[а(I, J) | Р], Были) :-

К is I+1,

можем_идти(a (K, J), Были),

путь(а(I, J) ,Р, [a(K, J) | Были]).

 /* Пытаемся идти на запад

путь(а (I, J), [a (I, J) | P], Были) :-

L is J-1,
можем_идти(а(I, L), Были),
путь(а(I, L), Р, [а(I, L)| Были]).
/* Пытаемся идти на восток
путь(а (I, J), [a (I, J) | P], Были) :-
L is J+1,
можем_идти(а(I, L), Были),
путь(а(I, L), Р, [а(I, L)| Были]).
/* в позицию a(I, J) можно попасть при
/* условии, что там нет стены и мы
/* не побывали в ней прежде
можем_идти(а(I, J)), Были) :-
отсутств_стена(I, J),
not (принадлежит (a (I, J), Были)).
Для того чтобы понять, каким образом процедура ищет путь к выходу, рассмотрим процесс согласования запроса с описанием лаби­ринта, описанного выше:
?-путь(а(4,2), Р, [а(4.2)]).
Выходом из лабиринта является позиция выход (3,1).
Выбор первого утверждения не приводит к согласованию целево­го утверждения, поскольку а (4,2) - не выход. Во втором утверждении делается попытка найти путь в северном направлении, т.е. согласовать целевое утверждение
путь(а(3, 2), Р2, [а(3, 2), а(4, 2)]).
Целевое утверждение не удается согласовать с первым утвержде­нием
путь(а(3, 2), Р2, [а(3, 2), а(4, 2)])
так как а (3,2) не является выходом. Во втором утверждении пред­принимается попытка найти путь, двигаясь на север, т.е. согласовать целевое утверждение
путь(а(2,2), РЗ, [а(2, 2), а(3, 2), а(4, 2)]).
Ни одно из утверждений не может согласовать
путь(а(2, 2), РЗ, [а(2, 2), а(3, 2), а(4, 2)]).
Первое утверждение - потому, что а (2, 2) не является выходом, вто­рое - потому, что северная позиция является стеной, третье утверждение - потому, что в южной позиции мы уже побывали, а четвертое и пятое утверждения - потому, что западная и восточная границы - это стены.
Неудача в согласовании
путь(а(2, 2), РЗ, [а(2, 2), а(3, 2), а(4, 2)])
заставляет Пролог-систему вернуться в ту точку, где было выбрано второе утверждение при попытке согласовать
путь(а(3, 2), Р2, [а(3, 2), а(4, 2)]).
Решение пересматривается и выбирается третье утверждение.
В третьем утверждении осуществляется попытка найти путь, двигаясь на юг, но она оказывается неудачной, поскольку мы уже по­бывали в позиции а (4, 2).Тогда, чтобы согласовать
путь(а(3, 2), Р2, [а(3, 2), а(4, 2)]),
выбирается четвертое утверждение. Мы успешно находим путь, дви­гаясь в западном направлении к позиции а(3,1), которая и является выходом. Рекурсия сворачивается, и в результате полу­чается путь
Р=[а(4, 2),а(3, 2), а(3,1)]
другие решения(да/нет)? да
Других решений нет
Альтернативный путь
[a(4,2), a(3,2), a(2,2), a(3,2), a(3,1)]
мы получить не можем, потому что не разрешается дважды бывать в одной и той же позиции.
Описанная процедура не обязательно находит кратчайший путь к выходу. Кратчайший путь можно найти, генерируя альтернативные пути с помощью вызова состояния неудачи и запоминая кратчайший из них.

Проблема обучения распознаванию образов (ОРО)

Одним из самых интересных свойств человеческого мозга является способность отвечать на бесконечное множество состояний внешней среды конечным числом реакций. Может быть, именно это свойство позволило человеку достигнуть высшей формы существования живой материи, выражающейся в способности к мышлению, т. е. активному отражению объективного мира в виде образов, понятий, суждений и т. д. Поэтому проблема ОРО возникла при изучении физиологических свойств мозга.

Рассмотрим пример задач из области ОРО.

Рис.  1

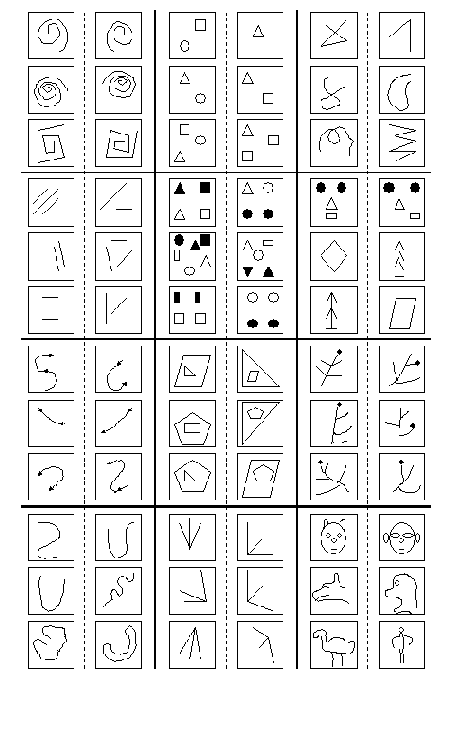
Здесь представлены 12 задач, в которых следует отобрать признаки, при помощи которых можно отличить левую триаду картинок от правой. Решение данных задач требует моделирования логического мышления в полном объеме.

В целом проблема распознавания образов состоит из двух частей: обучения и распознавания. Обучение осуществляется путем показа отдельных объектов с указанием их принадлежности тому или другому образу. В результате обучения распознающая система должна приобрести способность реагировать одинаковыми реакциями на все объекты одного образа и различными — на все объекты различных образов. Очень важно, что процесс обучения должен завершиться только путем показов конечного числа объектов без каких-либо других подсказок. В качестве объектов обучения могут быть либо картинки, либо другие визуальные изображения (буквы), либо различные явления внешнего мира, например звуки, состояния организма при медицинском диагнозе, состояние технического объекта в системах управления и др. Важно, что в процессе обучения указываются только сами объекты и их принадлежность образу. За обучением следует процесс распознавания новых объектов, который характеризует действия уже обученной системы. Автоматизация этих процедур и составляет проблему обучения распознаванию образов. В том случае, когда человек сам разгадывает или придумывает, а затем навязывает машине правило классификации, проблема распознавания решается частично, так как основную и главную часть проблемы (обучение) человек берет на себя.

Проблема обучения распознаванию образов интересна как с прикладной, так и с принципиальной точки зрения. С прикладной точки зрения решение этой проблемы важно прежде всего потому, что оно открывает возможность автоматизировать многие процессы, которые до сих пор связывали лишь с деятельностью живого мозга. Принципиальное значение проблемы тесно связано с вопросом, который все чаще возникает в связи с развитием идей кибернетики: что может и что принципиально не может делать машина? В какой мере возможности машины могут быть приближены к возможностям живого мозга? В частности, может ли машина развить в себе способность перенять у человека умение производить определенные действия в зависимости от ситуаций, возникающих в окружающей среде? Пока стало ясно только то, что если человек может сначала сам осознать свое умение, а потом его описать, т. е. указать, почему он производит действия в ответ на каждое состояние внешней среды или как (по какому правилу) он объединяет отдельные объекты в образы, то такое умение без принципиальных трудностей может быть передано машине. Если же человек обладает умением, но не может объяснить его, то остается только один путь передачи умения машине — обучение примерами.

Круг задач, которые могут решаться с помощью распознающих систем, чрезвычайно широк. Сюда относятся не только задачи распознавания зрительных и слуховых образов, но и задачи распознавания сложных процессов и явлений, возникающих, например, при выборе целесообразных действий руководителем предприятия или выборе оптимального управления технологическими, экономическими, транспортными или военными операциями. В каждой из таких задач анализируются некоторые явления, процессы, состояния внешнего мира, всюду далее называемые объектами наблюдения. Прежде чем начать анализ какого-либо объекта, нужно получить о нем определенную, каким-либо способом упорядоченную информацию. Такая информация представляет собой характеристику объектов, их отображение на множестве воспринимающих органов распознающей системы.



Но каждый объект наблюдения может воздействовать по-разному, в зависимости от условий восприятия. Например, какая-либо буква, даже одинаково написанная, может в принципе как угодно смещаться относительно воспринимающих органов. Кроме того, объекты одного и того же образа могут достаточно сильно отличаться друг от друга и, естественно, по-разному воздействовать на воспринимающие органы.

Каждое отображение какого-либо объекта на воспринимающие органы распознающей системы, независимо от его положения относительно этих органов, принято называть изображением объекта, а множества таких изображений, объединенные какими-либо общими свойствами, представляют собой образы.

При решении задач управления методами распознавания образов вместо термина "изображение" применяют термин "состояние". Состояние — это определенной формы отображение измеряемых текущих (или мгновенных) характеристик наблюдаемого объекта. Совокупность состояний определяет ситуацию. Понятие "ситуация" является аналогом понятия "образ". Но эта аналогия не полная, так как не всякий образ можно назвать ситуацией, хотя всякую ситуацию можно назвать образом.

Ситуацией принято называть некоторую совокупность состояний сложного объекта, каждая из которых характеризуется одними и теми же или схожими характеристиками объекта. Например, если в качестве объекта наблюдения рассматривается некоторый объект управления, то ситуация объединяет такие состояния этого объекта, в которых следует применять одни и те же управляющие воздействия. Если объектом наблюдения является военная игра, то ситуация объединяет все состояния игры, которые требуют, например, мощного танкового удара при поддержке авиации.

Выбор исходного описания объектов является одной из центральных задач проблемы ОРО. При удачном выборе исходного описания (пространства признаков) задача распознавания может оказаться тривиальной и, наоборот, неудачно выбранное исходное описание может привести либо к очень сложной дальнейшей переработку информации, либо вообще к отсутствию решения.Например, если решается задача распознавания объектов, отличающихся по цвету, а в качестве исходного описания выбраны сигналы, получаемые от датчиков веса, то задача распознавания в принципе не может быть решена.

Продукционные модели

В подобных случаях для обеспечения динамичности процессов модификации программ используются те или иные варианты таблиц решений. С учетом этого для исходной задачи более приемлемо решение 2:

Таблица 1. Решение 2

Ситуация	Действие	Ситуация	Действие
КИНО	КИНО	-Ь	-И
-ча	-чи	-ие	-ия
-КА	-КИ	-мя	-мени
-А	-Ы	-я	-и
-АРЬ	-АРЯ	-	-А
-Ь & М:хЬ	-Я

Соответствующая таблица решений содержит две графы — слева приведены описания ситуаций, справа — соответствующие действия. Предполагается, что программист разработал интерпретирующую программу для подобных таблиц. Эта программа работает следующим образом. Для конкретного входного слова, пусть это будет для примера слово РОЗА, осуществляется последовательный просмотр ситуаций, указанных в таблице, и сравнение их со входным словом. Если слово соответствует некоторой ситуации, то выполняется действие, указанное для этой ситуации.

Для слова РОЗА будет обнаружено соответствие с ситуацией "-А". В результате выполнения действия "-Ы" будет получено выходное слово РОЗЫ.

Теперь значительно упрощается расширение на новые классы слов — необходимо лишь обеспечить внесение вставок на нужное место в таблице решений.

Таблицы решений представляют собой частный случай так называемых продукционных систем. В этих системах правила вычислений представляются в виде продукций. Продукции представляют собой операторы специального вида и состоят из двух основных частей, для краткости называемых обычно "ситуация — действие".

"Ситуация" содержит описание ситуации, в которой применима продукция. Это описание задается в виде условий, называемых посылками продукции. "Действие" — это набор инструкций, подлежащих выполнению в случае применимости продукции.

Продукционные системы с исключениями

Если отношение "правило—исключение" встроено в систему, она сама может понять, что преобразование ПАЛКА à ПАЛКЫ незаконно. При этом система должна руководствоваться простым принципом: если применимо исключение, общее правило запрещено. Соответствующие системы будем называть системами с исключениями.

Отношение "общее правило — исключение" безусловно полезно для понимания системой уместности правил. Можно сказать, что это отношение устанавливает автоматически (по умолчанию) наиболее типичное для неформальных процедур взаимодействие правил:

— исключение "вытесняет" общее правило.

— при пересечении разрешены оба правила.

Разумеется, возможны ситуации, когда необходимо поступать наоборот:

— исключение не запрещает общего правила

— при пересечении одно из правил запрещено.

Пусть дано, например, общее правило х à р­1 и его исключение Ах à р2. Таким образом, для произвольного слова необходима реакция р1. Для слова же, начинающегося с буквы А, исполняется реакция р2 — по умолчанию для таких слов реакция р1 незаконна.

Предположим, однако, что по условию конкретной задачи для слов, начинающихся с А, реакция р1 также допустима. В этом случае введение нового правила Ах à р1 снимает запрет на реакцию р1 в ситуации Ах.

Аналогичный способ годится для пересечения правил.

Таким образом, аппарат исключений позволяет устанавливать произвольные способы взаимодействия правил, в том числе и отличные от взаимодействия по умолчанию.

При развитии продукционной системы с исключениями программист сосредотачивает свое внимание на выявлении новых правил и на обобщении уже имеющихся. Аппарат исключений освобождает программиста от решения трудоемких вопросов согласования правил — распознавание и интерпретация исключений осуществляется автоматически.

Пролог

Данную главу нельзя рассматривать как учебник по языку Пролог, а только как краткий "ликбез", служащий для иллюстрации принципов продукционного программирования, описанных выше.

Различные подходы к построению систем ИИ

Существуют различные подходы к построению систем ИИ. Это разделение не является историческим, когда одно мнение постепенно сменяет другое, и различные подходы существуют и сейчас. Кроме того, поскольку по-настоящему полных систем ИИ в настоящее время нет, то нельзя сказать, что какой-то подход является правильным, а какой-то ошибочным.

Для начала кратко рассмотрим логический подход. Почему он возник? Ведь человек занимается отнюдь не только логическими измышлениями. Это высказывание конечно верно, но именно способность к логическому мышлению очень сильно отличает человека от животных.

Основой для данного логического подхода служит Булева алгебра. Каждый программист знаком с нею и с логическими операторами с тех пор, когда он осваивал оператор IF. Свое дальнейшее развитие Булева алгебра получила в виде исчисления предикатов — в котором она расширена за счет введения предметных символов, отношений между ними, кванторов существования и всеобщности. Практически каждая система ИИ, построенная на логическом принципе, представляет собой машину доказательства теорем. При этом исходные данные хранятся в базе данных в виде аксиом, правила логического вывода как отношения между ними. Кроме того, каждая такая машина имеет блок генерации цели, и система вывода пытается доказать данную цель как теорему. Если цель доказана, то трассировка примененных правил позволяет получить цепочку действий, необходимых для реализации поставленной цели. Мощность такой системы определяется возможностями генератора целей и машиной доказательства теорем.

Конечно можно сказать, что выразительности алгебры высказываний не хватит для полноценной реализации ИИ, но стоит вспомнить, что основой всех существующих ЭВМ является бит — ячейка памяти, которая может принимать значения только 0 и 1. Таким образом было бы логично предположить, что все, что возможно реализовать на ЭВМ, можно было бы реализовать и в виде логики предикатов. Хотя здесь ничего не говорится о том, за какое время.

Добиться большей выразительности логическому подходу позволяет такое сравнительно новое направление, как нечеткая логика.
Основным ее отличием является то, что правдивость высказывания может принимать в ней кроме да/нет (1/0) еще и промежуточные значения — не знаю (0.5), пациент скорее жив, чем мертв (0.75), пациент скорее мертв, чем жив (0.25). Данный подход больше похож на мышление человека, поскольку он на вопросы редко отвечает только да или нет. Хотя правда на экзамене будут приниматься только ответы из разряда классической булевой алгебры.

Для большинства логических методов характерна большая трудоемкость, поскольку во время поиска доказательства возможен полный перебор вариантов. Поэтому данный подход требует эффективной реализации вычислительного процесса, и хорошая работа обычно гарантируется при сравнительно небольшом размере базы данных.

Под структурным подходом мы подразумеваем здесь попытки построения ИИ путем моделирования структуры человеческого мозга. Одной из первых таких попыток был перцептрон Френка Розенблатта. Основной моделируемой структурной единицей в перцептронах (как и в большинстве других вариантов моделирования мозга) является нейрон.

Позднее возникли и другие модели, которые в простонародье обычно известны под термином "нейронные сети" (НС). Эти модели различаются по строению отдельных нейронов, по топологии связей между ними и по алгоритмам обучения. Среди наиболее известных сейчас вариантов НС можно назвать НС с обратным распространением ошибки, сети Хопфилда, стохастические нейронные сети.

НС наиболее успешно применяются в задачах распознавания образов, в том числе сильно зашумленных, однако имеются и примеры успешного применения их для построения собственно систем ИИ, это уже ранее упоминавшийся ТАИР.

Для моделей, построенных по мотивам человеческого мозга характерна не слишком большая выразительность, легкое распараллеливание алгоритмов, и связанная с этим высокая производительность параллельно реализованных НС. Также для таких сетей характерно одно свойство, которое очень сближает их с человеческим мозгом — нейронные сети работают даже при условии неполной информации об окружающей среде, то есть как и человек, они на вопросы могут отвечать не только "да" и "нет" но и "не знаю точно, но скорее да".



Довольно большое распространение получил и эволюционный подход. При построении систем ИИ по данному подходу основное внимание уделяется построению начальной модели, и правилам, по которым она может изменяться (эволюционировать). Причем модель может быть составлена по самым различным методам, это может быть и НС и набор логических правил и любая другая модель. После этого мы включаем компьютер и он, на основании проверки моделей отбирает самые лучшие из них, на основании которых по самым различным правилам генерируются новые модели, из которых опять выбираются самые лучшие и т. д.

В принципе можно сказать, что эволюционных моделей как таковых не существует, существует только эволюционные алгоритмы обучения, но модели, полученные при эволюционном подходе имеют некоторые характерные особенности, что позволяет выделить их в отдельный класс.

Такими особенностями являются перенесение основной работы разработчика с построения модели на алгоритм ее модификации и то, что полученные модели практически не сопутствуют извлечению новых знаний о среде, окружающей систему ИИ, то есть она становится как бы вещью в себе.

Еще один широко используемый подход к построению систем ИИ — имитационный. Данный подход является классическим для кибернетики с одним из ее базовых понятий — "черным ящиком" (ЧЯ). ЧЯ — устройство, программный модуль или набор данных, информация о внутренней структуре и содержании которых отсутствуют полностью, но известны спецификации входных и выходных данных. Объект, поведение которого имитируется, как раз и представляет собой такой "черный ящик". Нам не важно, что у него и у модели внутри и как он функционирует, главное, чтобы наша модель в аналогичных ситуациях вела себя точно так же.

Таким образом здесь моделируется другое свойство человека — способность копировать то, что делают другие, не вдаваясь в подробности, зачем это нужно. Зачастую эта способность экономит ему массу времени, особенно в начале его жизни.

Основным недостатком имитационного подхода также является низкая информационная способность большинства моделей, построенных с его помощью.



С ЧЯ связана одна очень интересная идея. Кто бы хотел жить вечно? Я думаю, что почти все ответят на этот вопрос "я".

Представим себе, что за нами наблюдает какое-то устройство, которое следит за тем, что в каких ситуациях мы делаем, говорим. Наблюдение идет за величинами, которые поступают к нам на вход (зрение, слух, вкус, тактильные, вестибулярные и т. д.) и за величинами, которые выходят от нас (речь, движение и др.). Таким образом человек выступает здесь как типичный ЧЯ.

Далее это устройство пытается отстроить какую-то модель таким образом, чтобы при определенных сигналах на входе человека, она выдавала на выходе те же данные, что и человек. Если данная затея будет когда-нибудь реализована, то для всех посторонних наблюдателей такая модель будет той же личностью, что и реальный человек. А после его смерти она, будет высказывать те мысли, которые предположительно высказывал бы и смоделированный человек.

Мы можем пойти дальше и скопировать эту модель и получить брата близнеца с точно такими же "мыслями".

Можно сказать, что "это конечно все интересно, но при чем тут я? Ведь эта модель только для других будет являться мной, но внутри ее будет пустота. Копируются только внешние атрибуты, но я после смерти уже не буду думать, мое сознание погаснет (для верующих людей слово "погаснет" необходимо заменить на "покинет этот мир") ". Что ж это так. Но попробуем пойти дальше.

Согласно философским представлениям автора данного курса, сознание представляет собой сравнительно небольшую надстройку над нашим подсознанием, которая следит за активностью некоторых центров головного мозга, таких как центр речи, конечной обработки зрительных образов, после чего "возвращает" эти образы на начальные ступени обработки данной информации. При этом происходит повторная обработка этих образов, мы как бы видим и слышим, что думает наш мозг. При этом появляется возможность мысленного моделирования окружающей действительности при нашем "активном" участии в данном процессе.


И именно наш процесс наблюдения за деятельностью этих немногих центров является тем, что мы называем сознанием. Если мы "видим" и "слышим" наши мысли, мы в сознании, если нет, то мы находимся в бессознательном состоянии.

Если бы мы смогли смоделировать работу именно этих немногих "сознательных" нервных центров (работа которых правда основана на деятельности всего остального мозга) в качестве одного ЧЯ, и работу "супервизора" в качестве другого ЧЯ, то можно было бы с уверенностью говорить, что "да, данная модель думает, причем так же, как и я". Здесь я ничего не хочу говорить о том, как получить данные о работе этих нервных центров, поскольку на мой взгляд сегодня нет ничего такого, что позволило бы следить за мозгом человека годами и при этом не мешало бы его работе и жизни.

И заканчивая беглое ознакомление с различными методами и подходами к построению систем ИИ, хотелось бы отметить, что на практике очень четкой границы между ними нет. Очень часто встречаются смешанные системы, где часть работы выполняется по одному типу, а часть по другому.

Режим возвратов

Таблица решений, приведенная на Таблица 1, иллюстрирует так называемую безвозвратную процедуру. В этом случае на каждом шаге выбирается единственное решение — так, для слова РОЗА таким решением будет РОЗЫ — проблема выбора решения не возникает. В общем случае неформальные процедуры являются многозначными, а правильность конкретного выбора, сделанного на некотором шаге, проверяется на следующих шагах. При этом используется так называемый режим возвратов.

а). МАТЬ   ——————>      ЛЮБИТ     ——————> ?

                            что делать?                                                                      кого?

б). МАТЬ   <——————      ЛЮБИТ     <—————— ?

                                кого?                                                                       что делать?

Пусть предложение начинается со слов МАТЬ ЛЮБИТ ... . Проанализировав эти слова в первоначальном предположении именительного падежа для слова МАТЬ, система вправе построить структуру, представленную в случае а). Если следующее слово после слова ЛЮБИТ представляет собой существительное в винительном падеже, например, вся фраза имеет вид МАТЬ ЛЮБИТ СЫНА, то эта структура является окончательной. Если же фраза имеет вид МАТЬ ЛЮБИТ СЫН, то возникает противоречие или, как говорят, сигнал неуспеха — очередное слово СЫН противоречит ожиданию прямого дополнения. В этом случае система должна вернуться на ближайший из предыдущих шагов, где можно принять другую альтернативу анализа. В данном примере это шаг анализа слова МАТЬ — система должна принять теперь альтернативу винительного падежа для этого слова. Далее будет построена структура, указанная в случае б).

Тривиальность рассмотренного примера убеждает в необходимости режима возвратов при реализации неформальных процедур.

СИНТАКСИС ОПЕРАТОРОВ

Структуры арности 1 и 2 могут быть записаны в операторной форме, если атом, используемый как главный функтор в структуре, объявить оператором (см. гл. 6).

СИНТАКСИС СПИСКОВ

В сущности, список есть не что иное, как некоторая структура арности 2. Данная структура становится интересной и чрезвычайно полезной в случае, когда вторая компонента тоже является списком. Вследствие важности таких структур в Прологе имеются специаль­ные средства для записи списков. Возможности обработки списков рассматриваются в разд. 5.1.

СИНТАКСИС СТРОК

Строка определяется как список кодов символов. Коды символов имеют особое значение в языках программирования. Они выступают как средство связи компьютера с внешним миром. В большинстве ре­ализации Пролога существует специальный синтаксис для записи строк. Он подобен синтаксису атомов. Строкой является любая по­следовательность символов, которые могут быть напечатаны (кроме двойных кавычек), заключенная в двойные кавычки. Двойные ка­вычки в пределах строки записываются дважды «».

В некоторых реализациях Пролога строки рассматриваются как определенный тип объектов подобно атомам или спискам. Для их об­работки вводятся специальные встроенные предикаты. В других реа­лизациях строки обрабатываются в точности так же, как списки, при этом используются встроенные предикаты для обработки списков. Поскольку все строки могут быть определены как атомы или как спи­ски целых чисел, и понятие строки является чисто синтаксическим, мы не будем более к нему возвращаться.

СЛОЖНЫЕ ТЕРМЫ, ИЛИ СТРУКТУРЫ

Структура состоит из атома, называемого главным функтором, и последовательности термов, называемых компонентами структуры. Компоненты разделяются запятыми и заключаются в круглые скобки.

Приведем примеры структурированных термов:

собака(рекс), родитель(Х,У).

Число компонент в структуре называется арностью структуры. Так, в данном примере структура собака имеет арность 1 (записыва­ется как собака/1), а структура родитель - арность 2 (родитель/2). Заметим, что атом можно рассматривать как структуру арности 0.

Для некоторых типов структур допустимо использование альтер­нативных форм синтаксиса. Это синтаксис операторов для структур арности 1 и 2, синтаксис списков для структур в форме списков и син­таксис строк для структур, являющихся списками кодов символов.

Списки

СПИСКОВАЯ ФОРМА ЗАПИСИ

Задачи, связанные с обработкой списков, на практике встречаются очень часто. Скажем, нам понадобилось составить список студентов, находящихся в аудитории. С помощью Пролога мы можем определить список как последовательность термов, заключенных в скобки. Приведем примеры правильно построенных списков Пролога:

[джек, джон, фред, джилл, джон]

[имя (джон, смит), возраст (джек, 24), X]

[Х.У.дата (12,январь, 1986) ,Х]

[]

Запись [H|T] определяет список, полученный добавлением Н в начало списка Т. Говорят, что Н - голова, а Т - хвост списка [HIT]. На вопрос

?-L=[a | [b, c, d]]. будет получен ответ

L=[a, b, c, d]

а на запрос

?-L= [a, b, c, d], L2=[2 | L]. - ответ

L=[a, b, c, d], L2- [2, a, b, c, d]

Запись [Н | Т] используется для того, чтобы определить голову и хвост списка. Так, запрос

?- [X | Y]=[a, b, c]. дает

Х=а, Y=[b, c]

Заметим, что употребление имен переменных Н и Т необязательно. Кроме записи вида [H|T], для выборки термов используются пе­ременные. Запрос

?-[a, X, Y]=[a, b, c].

определит значения

X=b

Y=c

а запрос

?- [личность(Х) | Т]=[личность(джон), а, b].

значения

Х=джон

Т=[а, Ь]

НЕКОТОРЫЕ СТАНДАРТНЫЕ ЦЕЛЕВЫЕ УТВЕРЖДЕНИЯ ДЛЯ ОБРАБОТКИ СПИСКОВ

Покажем на примерах, как можно использовать запись вида [Н | T] вместе с рекурсией для определения некоторых полезных це­левых утверждений для работы со списками,

Принадлежность списку. Сформулируем задачу проверки при­надлежности данного терма списку.

Граничное условие:

Терм R содержится в списке [H|T], если R=H.

Рекурсивное условие:

Терм R содержится в списке [H|T], если R содержится в списке Т.

Первый вариант записи определения на Прологе имеет вид:

содержится (R, L) :-

L=[H I T],

H=R.

содержится(Р, L) :-

L=[H|T],

содержится (R, T).

Цель L=[H I T] в теле обоих утверждений служит для того, чтобы разделить список L на голову и хвост.

Можно улучшить программу, если учесть тот факт, что Пролог сначала сопоставляет с целью голову утверждения, а затем пытается согласовать его тело.
Новая процедура, которую мы назовем принад­лежит, определяется таким образом:

принадлежит (R, [R | Т]).

принадлежит (R, [H | Т]) :- принадлежит (R, T).

На запрос

?- принадлежит(а, [а, Ь, с]).

будет получен ответ

да

на запрос

?- принадлежит(b, [a, b, с]).

- ответ

да

но на запрос

?- принадлежит(d, (a, b, c)).

Пролог дает ответ

нет

В большинстве реализации Пролога предикат принадлежит яв­ляется встроенным.

Соединение двух списков. Задача  присоединения списка Q к списку Р, в результате чего получается список R, формулируется следующим образом:

Граничное условие:

Присоединение списка Q к [] дает Q.

Рекурсивное условие:

Присоединение списка Q к концу списка Р выполняется так: Q присоединяется к хвосту Р, а затем спереди добавляется голова Р.

Определение можно непосредственно написать на Прологе:

соединить([],0,0).

соединить(Р,Q,Р) :-

Р=[НР | ТР],

соединить(TP, Q, TR),

R=[HP | TR].

Однако, как и в предыдущем примере, воспользуемся тем, что Пролог сопоставляет с целью голову утверждения, прежде чем пы­таться согласовать тело:

присоединить([] ,Q,Q).

присоединить(HP | TP], Q, [HP | TR]) :-

присоединить (TP, Q, TR).

На запрос

?- присоединить [а, b, с], [d, e], L).

будет получен ответ

L = [a, b, c, d].

но на запрос

?- присоединить([a, b], [c, d], [e, f]).

ответом будет

нет

Часто процедура присоединить используется для получения спи­сков, находящихся слева и справа от данного элемента:

присоединить (L [джим, р], [джек,.билл, джим, тим, джим, боб] ) .

L = [джек, билл]

R = [тим, джим, боб]

другие решения (да/нет)? да

L=[джек, билл, джим, тим]

R=[боб]

другие решения (да/нет)? да

других решений нет

Индексирование списка. Задача получения N-ro терма в списке определяется следующим образом:

Граничное условие:

Первый терм в списке [Н | Т] есть Н.

Рекурсивное условие:

N-й терм в списке [Н | Т] является (N-I)-м термом в списке Т.

Данному определению соответствует программа:

/* Граничное условие:

получить ([H | Т], 1, Н). /* Рекурсивное условие:



получить([Н | Т], N, У) :-

М is N - 1,

получить (Т, М ,Y).

Построение списков из фактов. Иногда бывает полезно предста­вить в виде списка информацию, содержащуюся в известных фактах. В большинстве реализации Пролога есть необходимые для этого пре­дикаты:

bagof(X,Y,L)    определяет список термов L, конкретизирующих переменную Х как аргумент предиката Y, которые делают истинным предикат Y

setof(X,Y,L)     все сказанное о предикате bagof относится и к setof, за исключением того, что список L отсортирован и из него удалены все повторения.

Если имеются факты:

собака(рекс).

собака (голди).

собака (фидо).

собака(реке).

то на запрос

?- bagof(D, co6aкa(D), L),

будет получен ответ

L=[реке, голди, фидо, рекс]

в то время как

?-setof(D, co6aкa(D), L). дает значение

L=[фидо, голди, рекc]

Пример: сложение многочленов

Теперь мы достаточно подготовлены к тому, чтобы использовать списки для решения задач. Вопрос, которым мы займемся, - пред­ставление и сложение многочленов.

Представление многочленов. Посмотрим, как можно предста­вить многочлен вида

Р(х)=3+3х-4х^3+2х^9

Q(х)=4х+х^2-3х^3+7х^4+8х^5

Заметим, что каждое подвыражение (такое, как Зх ^3, Зх, 3) имеет самое большее две переменные компоненты: число, стоящее перед х, называемое коэффициентом, и число, стоящее после ^ - сте­пень. Следовательно, подвыражение представляется термом

х(Коэффициент, Степень)

Так, 5х^2 записывается как х(5,2), х^З представляется как х(1,3), а поскольку х^0 равно 1, подвыражению 5 соответствует терм х(5,0).

Теперь запишем многочлен в виде списка. Приведенный выше многочлен Р(х), например, будет выглядеть следующим образом:

[x(3, 0), '+', x(3, l), '-', x(4, 3), '+', x(2, 9)]

Воспользуемся тем, что многочлен

3 + 3х - 4х^3 + 2х^9

допускает замену на эквивалентный

3 + 3х + (-4)х^3 + 2х^9 Тогда он выражается списком:

[х(3, 0), '+', х(3, 1), '+', х(-4, 3), '+', х(2, 9)]

В такой записи между термами всегда стоят знаки '+'. Следователь­но, их можно опустить, и многочлен принимает окончательный вид:



[х(3, 0), х(3, 1), х(-4, 3), х(2, 9)]

Подразумевается, что между всеми термами списка стоят знаки '+'. Представлением многочлена Q(x) будет

[х(4, 1), х(1, 2), х(-3, 3), х(7, 4), х(8, 5)]

Сложение многочленов. Теперь напишем целевые утверждения для сложения двух многочленов. Сложение многочленов

3-2х^2+4х^3+6х^6

-1+3х^2-4х^3

в результате дает

2+х^2+6х^6

Аргументами целевого утверждения являются многочлены, пред­ставленные в виде списков. Ответ будет получен также в виде списка.

Сложение многочлена Р с многочленом Q осуществляется следу­ющим образом:

Граничное условие:

Р, складываемый с [], дает Р.

[], складываемый с Q, дает Q.

Рекурсивное условие:

При сложении Р с Q, в результате чего получается многочлен R, возможны 4 случая:

а) степень первого терма в Р меньше, чем степень первого терма в Q. В этом случае первый терм многочлена Р образует первый терм в R, а хвост R получается при прибавлении хвоста Р к Q. Например, если Р и Q имеют вид

Р(х)=3х^2+5х^3

Q(x)=4x^3+3x^4

то первый терм R(x) равен 3х^2 (первому терму в Р(х)). Хвост R(x) равен 9х^3+3х^4, т.е. результату сложения Q(x) и хвоста Р(х);

б) степень первого терма в Р больше степени первого терма в Q. В данном случае первый терм в Q образует первый терм в R, а хвост R получается при прибавлении Р к хвосту Q. Например, если

Р(х)=2х^3+5х^'4

Q(x)=3x^3-x^4

то первый терм R(x) равен 3х^2 (первому терму в Q(x)), а хвост R(x) равен 2х^3+4х^4 (результату сложения Р(х) и хвоста Q(x));

в) степени первых термов в Р и Q равны, а сумма их коэффици­ентов отлична от нуля. В таком случае первый терм в R имеет коэф­фициент, равный сумме коэффициентов первых термов в Р и Q. Сте­пень первого терма в R равна степени первого терма в Р (или Q). Хвост R получается при сложении хвоста Р и хвоста Q. Например, если Р и Q имеют вид

Р(х)=2х+3х^3

Q(x)=3x+4x^4

то первый терм многочлена R (х) равен 5х (результату сложения пер­вого терма в Р(х) с первым термом в Q(x)). Хвост R(x) равен 3х^3+4х^4 (результату сложения хвоста Р(х) и хвоста Q(x));



г) степени первых термов в Р и Q одинаковы, но сумма коэффи­циентов равна нулю. В данном случае многочлен R равен результату сложения хвоста Р с хвостом Q. Например, если

р(х)=2+2х

Q(x)=2-3x^2

то

R(x)=2x-3x^2

(это результат сложения хвостов многочленов Р (х) и Q (х)).

Рассмотренный процесс сложения многочленов можно непосред­ственно записать на языке Пролог:

/* Граничные условия

слож_мн([], Q Q).

слож_мн(P, [], P).

/* Рекурсивное условие

/* (a)

слож_мн([x(Pc, Pp)|Pt], [x(Qc, Qp)|Qt],

[x(Pc,Pp)IRt]) :-

PpQp,

слож_мн(Рt, [х(Qс,Qр) | Qt], Rt).

/*(б)

слож_мн([x(Pc, Pp) | Pt], [x(Qc, Qp) | Qt],

[x(Qc, Qp) | Rt]) :-

PpQp,

слож_мн([x(Pc, Pp) | Pt], Qt, Rt).

/*(в)

слож_мн([x(Pc, Pp) | Pt], [х(Qc,Pp) | Qt],

[x(Rc, Pp) | Rt]) :-

Rc is Pc+Qc,

Rc =\= 0,

слож_мн(Pt, Qt,Rt).

/*(r)

слож_мн([х(Рс, Рр) | Pt],

[x(Qc.Pp) | Qt], Rt) :-

Re is Pc+Qc,

Rc =:= 0,

слож_мн(Pt, Qt, Rt).

Заметим, что в двух последних утверждениях проверка на равен­ство осуществляется следующим образом: степени первых термов складываемых утверждений обозначает одна и та же переменная Pp.

Списки как термы. В начале главы мы упомянули о том, что спи­сок представляется с помощью терма. Такой терм имеет функтор '.', Два аргумента и определяется рекурсивно. Первый аргумент являет­ся головой списка, а второй - термом, обозначающим хвост списка. Пустой список обозначается []. Тогда список [а, b] эквивалентен терму.(а,.(b, [])).

Таким образом, из списков, как и из термов, можно создавать вложенные структуры. Поэтому выражение

[[a, b], [c, d], [a], a]

есть правильно записанный список, и на запрос

?- [Н | Т]=[[а, b], с].

Пролог дает ответ

Н=[а, b]

Т=[с]

Сравнение результатов арифметических выражений

Системные предикаты =:=, =\=, >, <, >= и <= определены как инфикс­ные операторы и применяются для сравнения результатов двух арифметических выражений.

Для предиката @ доказательство целевого утверждения X@Y за­канчивается успехом, если результаты вычисления арифметических выражений Х и Y находятся в таком отношении друг к другу, кото­рое задается предикатом @.

Такое целевое утверждение не имеет побочных эффектов и не может быть согласовано вновь. Если Х или Y - не арифметические выражения, возникает ошибка.

С помощью предикатов описываются следующие отношения:

Х =:= Y                   Х равно Y

Х =\= Y                   Х не равно Y

Х < Y                      Х меньше Y

Х > Y                      Х больше Y

Х <= Y                    Х меньше или равно Y

Х >= Y                    Х больше или равно Y

Использование предикатов иллюстрируют такие примеры:

а > 5                        заканчивается неудачей

5+2+7 > 5+2           заканчивается успехом

3+2 =:= 5                заканчивается успехом

3+2 < 5                    заканчивается неудачей

2 + 1 =\= 1              заканчивается успехом

N > 3                       заканчивается успехом, если N больше 3, и неудачей в противном случае

Структуры данных

Термы Пролога позволяют выразить самую разнообразную ин­формацию. В настоящей главе мы рассмотрим два вида широко ис­пользуемых структур данных: списки и бинарные деревья, и пока­жем, как они представляются термами Пролога.

Терминология

Термин интеллект (intelligence) происходит от латинского intellectus — что означает ум, рассудок, разум; мыслительные способности человека. Соответственно искусственный интеллект (artificial intelligence) — ИИ (AI) обычно толкуется как свойство автоматических систем брать на себя отдельные функции интеллекта человека, например, выбирать и принимать оптимальные решения на основе ранее полученного опыта и рационального анализа внешних воздействий.

Мы, в нашем курсе, интеллектом будем называть способность мозга решать (интеллектуальные) задачи путем приобретения, запоминания и целенаправленного преобразования знаний в процессе обучения на опыте и адаптации к разнообразным обстоятельствам.

В этом определении под термином "знания" подразумевается не только ту информацию, которая поступает в мозг через органы чувств. Такого типа знания чрезвычайно важны, но недостаточны для интеллектуальной деятельности. Дело в том, что объекты окружающей нас среды обладают свойством не только воздействовать на органы чувств, но и находиться друг с другом в определенных отношениях. Ясно, что для того, чтобы осуществлять в окружающей среде интеллектуальную деятельность (или хотя бы просто существовать), необходимо иметь в системе знаний модель этого мира. В этой информационной модели окружающей среды реальные объекты, их свойства и отношения между ними не только отображаются и запоминаются, но и, как это отмечено в данном определении интеллекта, могут мысленно "целенаправленно преобразовываться". При этом существенно то, что формирование модели внешней среды происходит "в процессе обучения на опыте и адаптации к разнообразным обстоятельствам".

Мы употребили термин интеллектуальная задача. Для того, чтобы пояснить, чем отличается интеллектуальная задача от просто задачи, необходимо ввести термин "алгоритм" — один из краеугольных терминов кибернетики.

Под алгоритмом понимают точное предписание о выполнении в определенном порядке системы операций для решения любой задачи из некоторого данного класса (множества) задач.
Термин "алгоритм" происходит от имени узбекского математика Аль-Хорезми, который еще в IX веке предложил простейшие арифметические алгоритмы. В математике и кибернетике класс задач определенного типа считается решенным, когда для ее решения установлен алгоритм. Нахождение алгоритмов является естественной целью человека при решении им разнообразных классов задач. Отыскание алгоритма для задач некоторого данного типа связано с тонкими и сложными рассуждениями, требующими большой изобретательности и высокой квалификации. Принято считать, что подобного рода деятельность требует участия интеллекта человека. Задачи, связанные с отысканием алгоритма решения класса задач определенного типа, будем называть интеллектуальными.

Что же касается задач, алгоритмы решения которых уже установлены, то, как отмечает известный специалист в области ИИ М. Минский, "излишне приписывать им такое мистическое свойства, как "интеллектуальность". В самом деле, после того, как такой алгоритм уже найден, процесс решения соответствующих задач становится таким, что его могут в точности выполнить человек, вычислительная машина (должным образом запрограммированная) или робот, не имеющие ни малейшего представления о сущность самой задачи. Требуется только, чтобы лицо, решающее задачу, было способно выполнять те элементарные операции, их которых складывается процесс, и, кроме того, чтобы оно педантично и аккуратно руководствовалось предложенным алгоритмом. Такое лицо, действуя, как говорят в таких случаях, чисто машинально, может успешно решать любую задачу рассматриваемого типа.

Поэтому представляется совершенно естественным исключить их класса интеллектуальных такие задачи, для которых существуют стандартные методы решения. Примерами таких задач могут служить чисто вычислительные задачи: решение системы линейных алгебраических уравнений, численное интегрирование дифференциальных уравнений и т. д. Для решения подобного рода задач имеются стандартные алгоритмы, представляющие собой определенную последовательность элементарных операций, которая может быть легко реализована в виде программы для вычислительной машины.


В противоположность этому для широкого класса интеллектуальных задач, таких, как распознавание образов, игра в шахматы, доказательство теорем и т. п., напротив это формальное разбиение процесса поиска решения на отдельные элементарные шаги часто оказывается весьма затруднительным, даже если само их решение несложно.

Таким образом, мы можем перефразировать определение интеллекта как универсальный сверхалгоритм, который способен создавать алгоритмы решения конкретных задач.

Еще интересным замечанием здесь является то, что профессия программиста, исходя из наших определений, является одной из самых интеллектуальных, поскольку продуктом деятельности программиста являются программы — алгоритмы в чистом виде. Именно поэтому, создание даже элементов ИИ должно очень сильно повысить производительность его труда.

Деятельность мозга (обладающего интеллектом), направленную на решение интеллектуальных задач, мы будем называть мышлением, или интеллектуальной деятельностью. Интеллект и мышление органически связаны с решением таких задач, как доказательство теорем, логический анализ, распознавание ситуаций, планирование поведения, игры и управление в условиях неопределенности. Характерными чертами интеллекта, проявляющимися в процессе решения задач, являются способность к обучению, обобщению, накоплению опыта (знаний и навыков) и адаптации к изменяющимся условиям в процессе решения задач. Благодаря этим качествам интеллекта мозг может решать разнообразные задачи, а также легко перестраиваться с решения одной задачи на другую. Таким образом, мозг, наделенный интеллектом, является универсальным средством решения широкого круга задач (в том числе неформализованных) для которых нет стандартных, заранее известных методов решения.

Следует иметь в виду, что существуют и другие, чисто поведенческие (функциональные) определения. Так, по А. Н. Колмогорову, любая материальная система, с которой можно достаточно долго обсуждать проблемы науки, литературы и искусства, обладает интеллектом.


Другим примером поведенческой трактовки интеллекта может служить известное определение А. Тьюринга. Его смысл заключается в следующем. В разных комнатах находится люди и машина. Они не могут видеть друг друга, но имеют возможность обмениваться информацией (например, с помощью электронной почты). Если в процессе диалога между участниками игры людям не удается установить, что один из участников — машина, то такую машину можно считать обладающей интеллектом.

Кстати интересен план имитации мышления, предложенный А. Тьюрингом. "Пытаясь имитировать интеллект взрослого человека, — пишет Тьюринг, — мы вынуждены много размышлять о том процессе, в результате которого человеческий мозг достиг своего настоящего состояния… Почему бы нам вместо того, чтобы пытаться создать программу, имитирующую интеллект взрослого человека, не попытаться создать программу, которая имитировала бы интеллект ребенка? Ведь если интеллект ребенка получает соответствующее воспитание, он становится интеллектом взрослого человека… Наш расчет состоит в том, что устройство, ему подобное, может быть легко запрограммировано… Таким образом, мы расчленим нашу проблему на две части: на задачу построения "программы-ребенка" и задачу "воспитания" этой программы".

Забегая вперед, можно сказать, что именно этот путь используют практически все системы ИИ. Ведь понятно, что практически невозможно заложить все знания в достаточно сложную систему. Кроме того, только на этом пути проявятся перечисленные выше признаки интеллектуальной деятельности (накопление опыта, адаптация и т. д.).

ТЕРМЫ

Объекты данных в Прологе называются термами. Терм может быть константой, переменной или составным термом (структурой). Константами являются целые и действительные числа, например:

0, -l, 123.4, 0.23E-5,

(некоторые реализации Пролога не поддерживают действительные числа).

К константам относятся также атомы, такие, как:

голди, а, атом, +, :, 'Фред Блогс', [].

Атом есть любая последовательность символов, заключенная в одинарные кавычки. Кавычки опускаются, если и без них атом мож­но отличить от символов, используемых для обозначения перемен­ных. Приведем еще несколько примеров атомов:

abcd, фред, ':', Джо.

Полный синтаксис атомов описан ниже.

Как и в других языках программирования, константы обознача­ют конкретные элементарные объекты, а все другие типы данных в Прологе составлены из сочетаний констант и переменных.

Имена переменных начинаются с заглавных букв или с символа подчеркивания "_". Примеры переменных:

X, Переменная, _3, _переменная.

Если переменная используется только один раз, необязательно называть ее. Она может быть записана как анонимная переменная, состоящая из одного символа подчеркивания "_". Переменные, подо­бно атомам, являются элементарными объектами языка Пролог.

Завершает список синтаксических единиц сложный терм, или структура. Все, что не может быть отнесено к переменной или кон­станте, называется сложным термом. Следовательно, сложный терм состоит из констант и переменных.

Теперь перейдем к более детальному описанию термов.

Указатели

I

intelligence............................................................. 1

artificial............................................................... 1

И

интеллект............................................................... 1

искусственный................................................ 1

интеллектуальная задача................................... 1

Унификация

Одним из наиболее важных аспектов программирования на Про­логе являются понятия унификации (отождествления) и конкретиза­ции переменных.

Пролог пытается отождествить термы при доказательстве, или согласовании, целевого утверждения. Например, в программе из гл. 1 для согласования запроса ?- собака(Х) целевое утверждение соба­ка (X) было отождествлено с фактом собака (реке), в результате чего переменная Х стала конкретизированной: Х= рекc.

Переменные, входящие в утверждения, отождествляются особым образом - сопоставляются. Факт доказывается для всех значений пе­ременной (переменных). Правило доказывается для всех значений переменных в головном целевом утверждении при условии, что хво­стовые целевые утверждения доказаны. Предполагается, что пере­менные в фактах и головных целевых утверждениях связаны кван­тором всеобщности. Переменные принимают конкретные значения на время доказательства целевого утверждения.

В том случае, когда переменные содержатся только в хвостовых целевых утверждениях, правило считается доказанным, если хвосто­вое целевое утверждение истинно для одного или более значений пе­ременных. Переменные, содержащиеся только в хвостовых целевых утверждениях, связаны квантором существования. Таким образом, они принимают конкретные значения на то время, когда целевое ут­верждение, в котором переменные были согласованы, остается дока­занным.

Терм Х сопоставляется с термом Y по следующим правилам. Ес­ли Х и Y - константы, то они сопоставимы, только если они одинако­вы. Если Х является константой или структурой, а Y - неконкретизи­рованной переменной, то Х и Y сопоставимы и Y принимает значе­ние Х (и наоборот). Если Х и Y - структуры, то они сопоставимы тог­да и только тогда, когда у них одни и те же главный функтор и ар­ность и каждая из их соответствующих компонент сопоставима. Если Х и Y - неконкретизированные (свободные) переменные, то они со­поставимы, в этом случае говорят, что они сцеплены. В (Таблица 2) при­ведены примеры отождествимых и неотождествимых термов.

Таблица 2. Иллюстрация унификации.

Терм1

Терм2

УТВЕРЖДЕНИЯ Программа на Прологе есть совокупность утверждений. Утверж­дения состоят из целей и хранятся в базе данных Пролога. Таким об­разом, база данных Пролога может рассматриваться как программа на Прологе. В конце утверждения ставится точка «.». Иногда утверж­дение называется предложением. Основная операция Пролога - доказательство целей, входящих в утверждение. Существуют два типа утверждений: факт: это одиночная цель, которая, безусловно, истинна; правило: состоит из одной головной цели и одной или более хво­стовых целей, которые истинны при некоторых условиях. Правило обычно имеет несколько хвостовых целей в форме конъ­юнкции целей. Конъюнкцию можно рассматривать как логическую функцию И. Таким образом, правило согласовано, если согласованы все его хво­стовые цели. Примеры фактов: собака(реке). родитель(голди.рекс). Примеры правил: собака (X) :- родитель (X.Y),собака (Y). человек(Х) :-мужчина(Х). Разница между правилами и фактами чисто семантическая. Хотя для правил мы используем синтаксис операторов (более подробное рассмотрение операторного и процедурного синтаксисов выходит за рамки нашего курса), нет ни­какого синтаксического различия между правилом и фактом. Так, правило собака (X) :- родитель(Х,У),собака(У). может быть задано как :-собака (X) ',' родитель(Х.У) .собака (Y). Запись верна, поскольку :- является оператором «при условии, что», а ',' - это оператор конъюнкции. Однако удобнее записывать это как собака (X) :-родитель (X.Y),собака (Y). и читать следующим образом: « Х - собака при условии, что родите­лем Х является Y и Y - собака». Структуру иногда изображают в виде дерева, число ветвей кото­рого равно арности структуры. Вспомогательные системы нижнего Для того, чтобы человек сознательно воспринял информацию (для примера возьмем чертеж), она должна пройти довольно длительный цикл предварительной обработки. Вначале свет попадает в глаз. Пройдя через всю оптическую систему фотоны в конце концов попадают на сетчатку — слой светочувствительных клеток — палочек и колбочек. Уже здесь — еще очень далеко от головного мозга, происходит первый этап обработки информации, поскольку, например, у млекопитающих, сразу за светочувствительными клетками находится обычно два слоя нервных клеток, которые выполняют сравнительно несложную обработку. Теперь информация поступает по зрительному нерву в головной мозг человека, в так называемые "зрительные бугры". То, что именно сюда приходит видеоинформация для дальнейшей обработки, показывают многочисленные опыты над людьми во время различных операций, в ходе которых производилась трепанация черепа. При этом пациентам раздражали область зрительных бугров слабым электрическим полем, что вызывало у них различные световые галлюцинации. Причем, что интересно, при изменении места раздражения, пропорционально смещению, смещались и места галлюцинаций, т. е. на зрительные бугры как бы проецируется то, что мы видим. Некоторые исследователи пошли дальше, и вживляли слепым людям целую матрицу электродов, напряжения на которых соответствовали освещенности соответствующих участков видеокамеры, размещенной на голове пациента. После операции, слепые начинали различать крупные фигуры (квадрат, треугольник, круг) и даже читать текст (при вживлении матрицы 10*10). Широкому распространению данного метода лечения слепоты препятствуют как недостаточно высокий наш технический уровень, так и чрезвычайно высокая опасность операций на открытом мозге. Такого рода опыты проводятся только попутно с операцией, вызванной другими причинами. Далее зрительная информация поступает в отделы мозга, которые уже выделяют из нее отдельные составляющие — горизонтальные, вертикальные, диагональные линии, контуры, области светлого, темного, цветного. До этих пор мы можем без труда смоделировать работу мозга применяя различные графические фильтры. Постепенно образы становятся все более сложными и размытыми, но графический образ картины пройдет еще долгий путь, прежде чем достигнет уровня сознания. Причем на уровне сознания у нас будет не только зрительный образ, к нему примешаются еще и звуки, запахи (если картина представляет собой натюрморт) и вкусовые ощущения. Дальнейшие ассоциации каждый может додумать сам. Смысл всего сказанного заключается в том, чтобы показать, что в системах ИИ имеются подсистемы, которые мы уже сейчас можем реализовать даже не зная о том, как они реализованы у человека. Причем можем это сделать не хуже, чем у прототипа, а зачастую и лучше. Например, искусственный глаз (а равно и блок первичной обработки видеоинформации, основанные на простейших фильтрах или др. сравнительно несложных устройствах) не устает, может видеть в любом диапазоне волн, легко заменяется на новый, видит при свете звезд. Устройства обработки звука позволяют улавливать девиацию голоса человека в 1-2 Герца. Данное изменение частоты происходит при повышенном возбуждении вегетативной нервной системы, которое в свою очередь часто обусловлено волнением человека. На данном принципе основаны современные детекторы лжи, которые позволяют обнаружить с высокой вероятностью даже записанные на пленку много лет назад ложные высказывания. Современные системы управления электродвигателем позволяют с высокой точностью держать заданные координаты даже при ударном изменении нагрузки. А ведь это примерно тоже, что держать на длинной палке баскетбольный мяч, по которому то слева, то справа кидают теннисные мячи. За одно и тоже время, компьютер произведет гораздо больше арифметических операций и с большей точностью, чем человек. Антиблокировочная система на автомобилях позволяет держать тормоза на грани заклинивания колеса, что дает наибольшее трение с дорогой, а это без АБС по силам только очень опытным водителям. В принципе такие примеры, где техника оказывается ничуть не хуже человека, можно продолжать до бесконечности. Общий же смысл сказанного в том, что при конструировании ИИ, мы не связаны одним набором элементарных составляющих, как природа. В каждом конкретном случае желательно применять то, что даст самый большой эффект. В той области, где у человека господствуют рефлексы (чихание, быстрое напряжение быстро растягиваемой мышцы, переваривание пищи, регулировка температуры), мы вообще можем применить жесткие системы управления, с раз и навсегда заданным алгоритмом функционирования. При этом вполне можно ожидать увеличения точности и уменьшение времени обучения их до нуля. При этом ядро нашей системы ИИ будет решать уже не настолько глобальные задачи. Данный принцип разбиения задачи на подзадачи уже давно используется природой. К примеру, мы далеко не полностью используем все возможности наших мышц в области разнообразия движений. Мы не можем заставить наши глаза смотреть в разные стороны, не говоря уже о том, чтобы делать это на разном уровне (левый глаз — влево-вверх, правый — вправо-вниз). При ходьбе мы часто используем далеко не оптимальный набор движений и далеко не все сочетания вариантов напряжения мышц мы опробуем. Попробуйте к примеру сделать волну животом. В принципе здесь нет ничего сложного, поскольку каждый пучок мышц пресса иннервируется отдельно, но если Вы этого не делали ранее, то получить необходимый результат будет не просто — в повседневной жизни это действие ненужно, а значит его нет и в "словаре движений", а на обучение необходимо определенное время. А по поводу оптимальности походки существуют расчеты, что если бы человек всегда рассчитывал оптимально траекторию движения в которой существует более 200 степеней свобод, то он бы не ходил, а в основном бы только думал о том, как надо ходить. На самом деле наша система управления построена по иерархическому принципу, когда задача распределяется между несколькими уровнями. Высший уровень нервной системы (связанный с большими полушариями мозга) ставит лишь общую задачу, скажем, переложить книгу на стол. Этот уровень вообще не контролирует действие отдельных двигательных единиц, направленных на решение поставленной задачи. Здесь уместна аналогия: командующий армией, ставя перед своими войсками некую общую задачу, отнюдь не предписывает каждому солдату и офицеру, что именно он должен делать в каждый момент операции. Детализация построения движений у человека происходит на уровнях более низких, чем командный уровень коры больших полушарий. Более того, в некоторых случаях (когда мы отдергиваем руку, прикоснувшись к горячему предмету, даже не успев осознать ситуацию) все управление формируется на нижележащих уровнях, связанных с различными отделами спинного мозга. В общем ситуация схожа с той, когда программист использует библиотеку подпрограмм. При этом ему не важно, какой алгоритм они используют, если программа работает нормально. А на написание своей библиотеки тратится драгоценное время. Кроме того, еще не известно, будет ли она работать так же хорошо. Общий вывод данной лекции состоит в том, что в настоящее время существуют методы, алгоритмы и устройства, которые позволяют нам довольно неплохо смоделировать нижние уровни человеческого интеллекта, причем совсем не обязательно на таком же физическом принципе. И если бы это была не лекция, а тост, то я бы закончил его: " …так выпьем же за протестированные, правильно работающие и бесплатные библиотеки подпрограмм". Язык Пролог не предназначен для Язык Пролог не предназначен для программирования задач с большим количеством арифметических операций. Для этого ис­пользуются процедурные языки программирования. Однако в лю­бую Пролог-систему включаются все обычные арифметические операторы: +              сложение —            вычитание *              умножение /               деление mod         остаток от деления целых чисел div           целочисленное деление В некоторых реализациях языка Пролог присутствует более ши­рокий набор встроенных арифметических операторов. Пролог позволяет также сравнивать арифметические выраже­ния, используя следующие встроенные предикаты: Диапазоны чисел, входящих в арифметические выражения, за­висят от реализации Пролога. Например, система ICLPROLOG опе­рирует с целыми числами со знаком в диапазоне –8388606 ... 8388607 ВВОД программ Введение списка утверждений в Пролог-систему осуществляется с помощью встроенного предиката consult. Аргументом предиката consult является атом, который обычно интерпретируется системой как имя файла, содержащего текст программы на Прологе. Файл от­крывается, и его содержимое записывается в базу данных. Если в файле встречаются управляющие команды, они сразу же выполня­ются. Возможен случай, когда файл не содержит ничего, кроме уп­равляющих команд для загрузки других файлов. Для ввода утверж­дений с терминала в большинстве реализации Пролога имеется спе­циальный атом, обычно user. С его помощью утверждения записыва­ются в базу данных, а управляющие команды выполняются немед­ленно. Помимо предиката consult, в Прологе существует предикат reconsult. Он работает аналогичным образом. Но перед добавлени­ем утверждений к базе данных из нее автоматически удаляются те утверждения, головные цели которых сопоставимы с целями, со­держащимися в файле перезагрузки. Такой механизм позволяет вводить изменения в базу данных. В Прологе имеются и другие методы добавления и удаления утверждений из базы данных. Не­которые реализации языка поддерживают модульную структуру, позволяющую разрабатывать модульные программы. В заключение раздела дадим формальное определение синтакси­са Пролога, используя форму записи Бэкуса-Наура, иногда называе­мую бэкусовской нормальной формой (БНФ). запрос ::- голова утверждения правило ::– голова утверждения :- хвост утверждения факт ::- голова утверждения голова утверждения ::-атом | структура хвост утверждения ::- атом структура, термы ::-терм [,термы] терм ::- число | переменная | атом | структура структура ::-атом (термы) Данное определение синтаксиса не включает операторную, спи­сковую и строковую формы записи. Полное определение дано в при­ложении А. Однако, любая программа на Прологе может быть напи­сана с использованием вышеприведенного синтаксиса. Специальные формы только упрощают понимание программы. Как мы видим, син­таксис Пролога не требует пространного объяснения. Но для написа­ния хороших программ необходимо глубокое понимание языка. Вычисление арифметических выражений В Прологе не допускаются присваивания вида Сумма=2+4. Выражение такого типа вычисляется только с помощью систем­ного предиката is, например: Сумма is 2 + 4. Предикат is определен как инфиксный оператор. Его левый аргу­мент - или число, или неконкретизированная переменная, а правый аргумент - арифметическое выражение. Попытка доказательства целевого утверждения Х is Y заканчи­вается успехом в одном из следующих случаев: а) Х - неконкретизированная переменная, а результат вычисле­ния выражения Y есть число; б) Х - число, которое равно результату вычисления выражения Y. Цель Х is Y не имеет побочных эффектов и не может быть согла­сована вновь. Если Х не является неконкретизированной переменной или числом, или если Y - не арифметическое выражение, возникает ошибка. Примеры: D is 10- 5                заканчивается успехом и D становится равным 5 4 is 2 * 4 - 4            заканчивается успехом 2 * 4 - 4 is 4            заканчивается неудачей a is 3 + 3                 заканчивается неудачей X is 4 + а                заканчивается неудачей 2 is 4 - X                 заканчивается неудачей Обратите внимание, что предикат is требует, чтобы его первый аргумент был числом или неконкретизированной переменной. Поэтому М - 2 is 3 записано неверно. Предикат is не является встроен­ным решателем уравнений. ЗАПРОСЫ После записи утверждений в базу данных вычисления могут быть инициированы вводом запроса. Запрос выглядит так же, как и целевое утверждение, образуется и обрабатывается по тем же правилам, но он не входит в базу данных (программу). В Прологе вычислительная часть программы и данные имеют одинаковый синтаксис. Программа обладает как декларатив­ной, так и процедурной семантикой. Мы отложим обсуждение этого вопроса до последующих глав. Запрос обозначается в Прологе утвер­ждением ?-, имеющим арность 1. Обычно запрос записывается в опе­раторной форме: за знаком ?- следует ряд хвостовых целевых утвер­ждений (чаще всего в виде конъюнкции). Приведем примеры запросов: ?-собака(X). ?- родитель(Х.У),собака (Y). или, иначе, '?-'(собака(Х)) С?-') ','(родитель(Х„У»,собака (Y)). Последняя запись неудобна тем, что разделитель аргументов в структуре совпадает с символом конъюнкции. Программисту нужно помнить о различных значениях символа ','. Запрос иногда называют управляющей командой (директивой), так как он требует от Пролог-системы выполнения некоторых дейст­вий. Во многих реализациях Пролога для управляющей команды ис­пользуется альтернативный символ, а символ ?- обозначает приглашение верхнего уровня интерпретатора Пролога. Альтернативным символом является :-. Таким образом, :-write(co6aкa). - это управляющая команда, в результате выполнения которой печа­тается атом собака. Управляющие команды будут рассмотрены ниже при описании ввода программ. Зависимость продукций Продукционные системы, содержащие аппарат логического вывода, отличает высокая степень общности правил обработки данных. Однако именно эта общность приводит к ухудшению динамических свойств соответствующих продукционных программ, к трудностям их модификации и развития. Чтобы понять, в чем тут причина, обратимся снова к Таблица 1. Пока эта таблица содержит несколько строк, не представляет особого труда установление правильного порядка их следования, но если учесть, что реальное количество продукций в подобных задачах исчисляется сотнями и более, трудоемкость их правильного взаимного расположения становится очевидной. Практически, при программировании неформальных "человеческих" процедур, подобные таблицы можно вручную создавать и сопровождать для нескольких десятков продукций, максимум — для 100-200 продукций. Продукции зависимы, и за правильное выявление этой зависимости отвечает программист. Новые продукции необходимо вручную вставлять на нужное место. Мы могли бы использовать в таблице решений только конкретные факты, например правила ДОМ à ДОМА, МАМА à МАМЫ и т. д., и динамичность соответствующей таблицы решений была бы восстановлена — подобные правила можно было бы вводить в произвольном порядке! Однако цена подобной "динамичности" окажется непомерно высокой — полный отказ от обобщенных правил. Желательно восстановить динамичность продукционно-логических систем, сохранив при этом в полном объеме возможность использования обобщенных правил. Продукционная система должна взять на себя функции распознавания и интерпретации приоритета продукций — программист должен только описывать ситуации и соответствующие им действия.